Se analizziamo i circuiti con Amplificatori Operazionali e soprattutto se vogliamo progettare un circuito che sia il più possibile preciso e privo di sorprese dobbiamo conoscere le limitazioni da imporre alla scelta dei componenti utilizzati nella rete di reazione.

Abbiamo già visto in un precedente articolo che l’ordine di grandezza delle resistenze impiegate non può essere arbitrario pena il mancato funzionamento “ideale” del circuito, ovvero le approssimazioni per cui si possono sfruttare le idealità dell’OpAmp non sono più valide. In particolare è stato mostrato in quali casi non è possibile applicare la semplificazione del “corto circuito virtuale”. Vedremo ora che anche scegliendo le resistenze dell’ordine dei chiloOhm vi sono delle ulteriori limitazioni. Iniziamo con il ricavare la caratteristica di trasferimento, cioè il guadagno. Consideriamo il circuito di Figura 1, in cui confrontiamo l’OpAmp reale OP492 della Analog Devices con un modello LTSpice ideale.

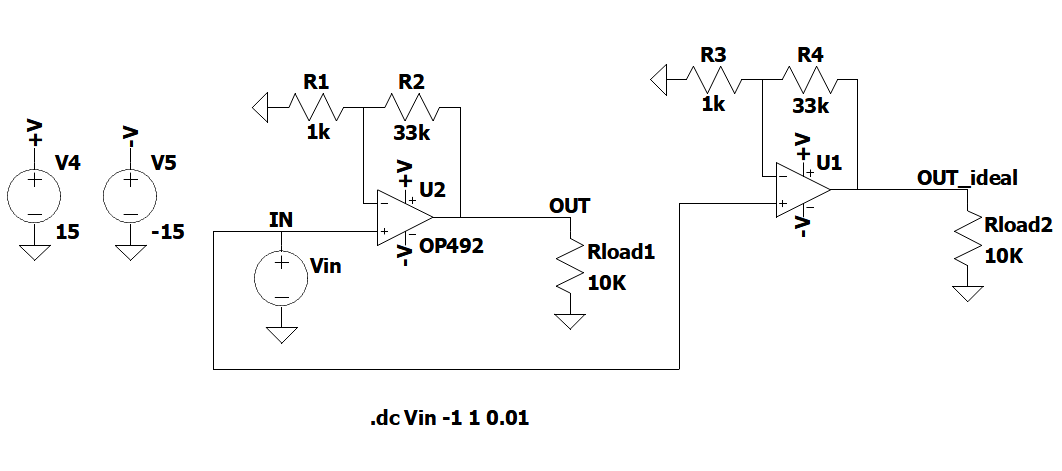
Figura 1

Guadagno non invertente

Applicando il principio del corto circuito virtuale avremo che V_– è uguale a Vin e pertanto Vout si può calcolare con la formula del partitore di tensione (se nel morsetto “–“ non entra corrente):

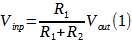
da cui si ricava la funzione di trasferimento ideale:

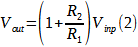
In realtà, dato che il guadagno A dell’amplificatore non è infinito, la tensione V_– = V₊ – eps, dove con eps si indica la tensione presente fra i morsetti “+“ e “-” che è pari a Vout/A. Di conseguenza la (1) deve essere riscritta:

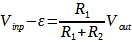
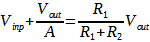
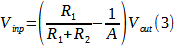
Nella (3) possiamo trascurare il termine 1/A e quindi considerare valida la (1) se A>>(1+R2/R1), che in termini pratici significa almeno 1000 volte maggiore (perché, per applicazioni “normali”, sono richieste almeno tre cifre significative). Di conseguenza, R2 ed R1 non possono essere scelti a piacere ma il loro rapporto ha un limite superiore. Assodato che R2>R1 (se vogliamo amplificare a sufficienza il segnale di ingresso) ed A è almeno 10⁴, si ha che R2/R1 può essere al massimo 10 per garantire la precisione richiesta. Ovviamente all’aumentare del guadagno questa condizione si rilassa ed è compito del progettista scegliere l’amplificatore con le caratteristiche adatte. Per mostrare gli effetti della scarsa precisione effettuiamo una DC analysis, facendo variare la Vin fra -1V e 1V, con il comando:

.dc Vin -1 1 0.01

come visibile in Figura 1, per differenti valori di R1, in modo da verificare il peggioramento delle prestazioni all’aumentare del guadagno (1). Nella prima simulazione R1=33k, per cui (1+R2/R1)= 2 e, come si vede dalla Figura 2, si vede come la tensione di uscita Vout non assuma esattamente i valori ideali attesi, ma presenti un offset in uscita di circa -16 mV.

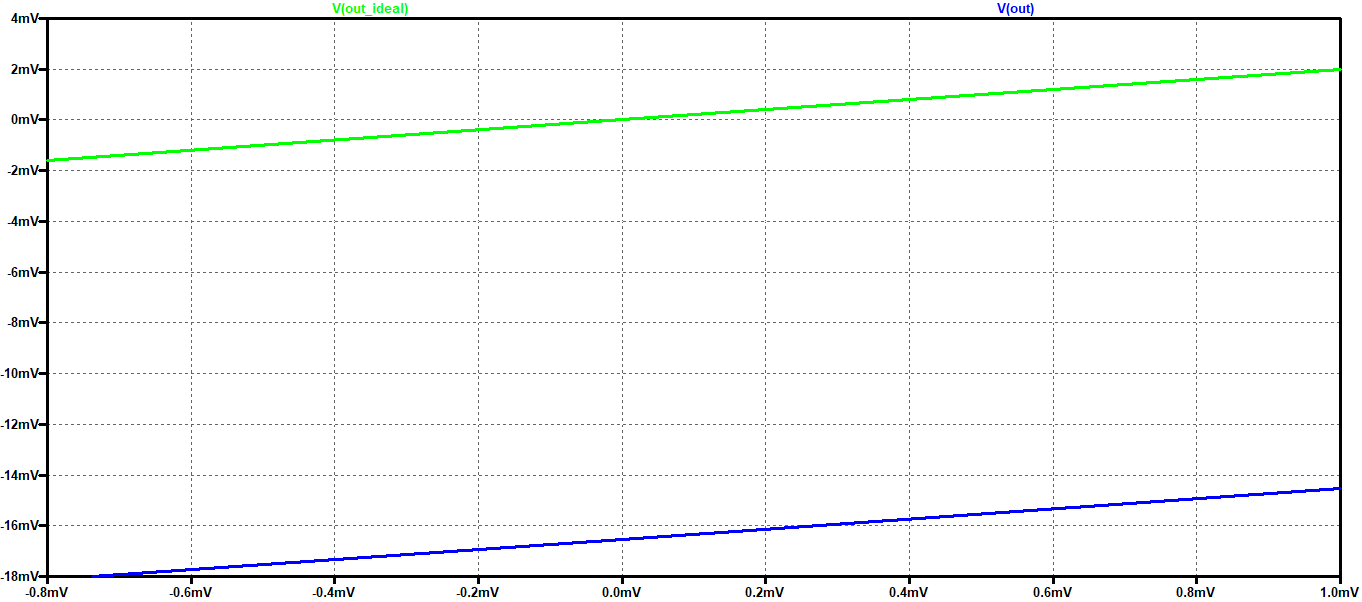
Figura 2

Ripetendo la simulazione con un valore di R1=3.3k (e guadagno pari a 11) le prestazioni peggiorano notevolmente, con un raddoppio della tensione di uscita come visibile in Figura 3:

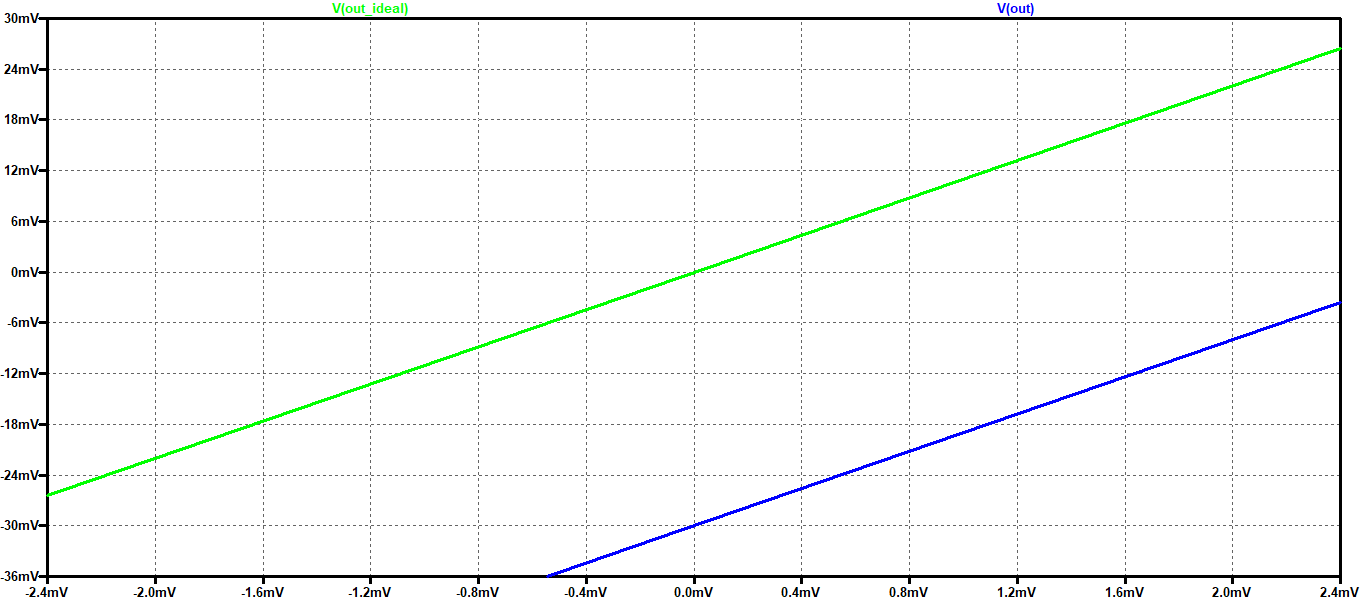
Figura 3

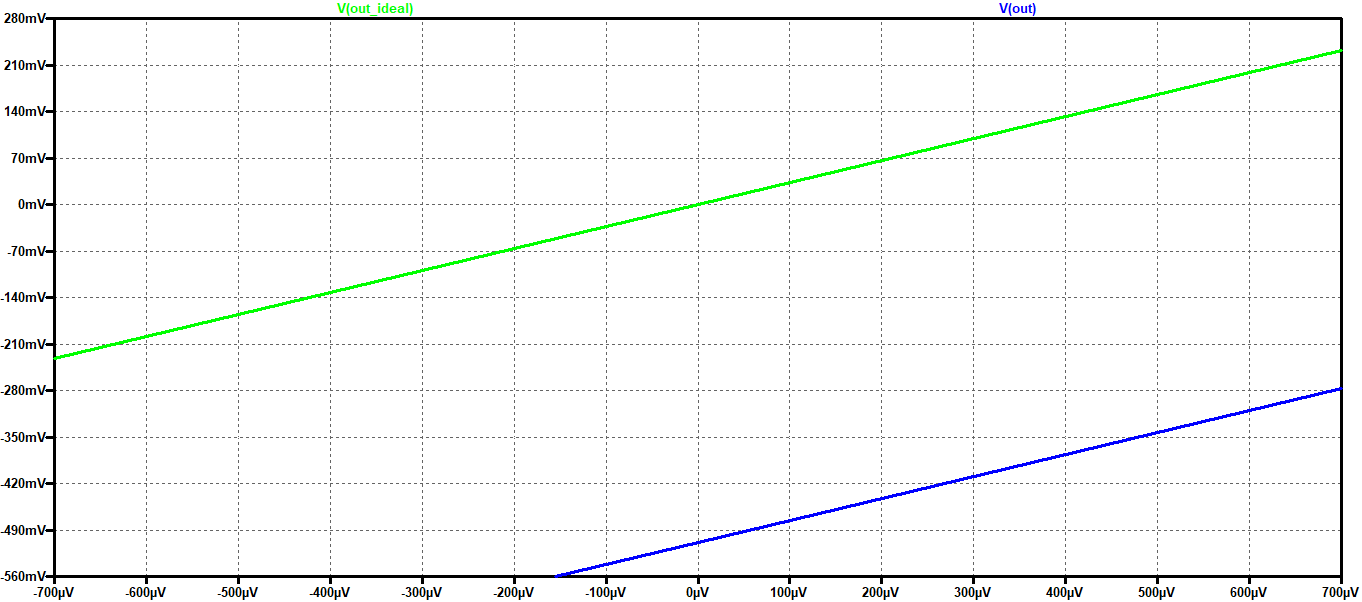
Figura 4

In questo caso limite abbiamo addirittura mezzo Volt di differenza fra ingresso ed uscita, che sicuramente non è accettabile per una applicazione in cui vogliamo rilevare segnali molto piccoli. Infatti con una amplificazione pari a 331 e con una saturazione di circa 15V (ricordiamo che l’uscita non può superare la tensione di alimentazione) si ha che l’uscita satura per un valore dell’ingresso di circa 45 mV. In pratica abbiamo un circuito che può amplificare segnali fra -45 e +45 mV ed abbiamo un errore in uscita di mezzo Volt. Praticamente inaccettabile, come predetto dalla teoria. Con questi esempi abbiamo anche visto che nel progettare un circuito possiamo fare delle approssimazioni utili a non perderci in calcoli matematici complicati, ma dobbiamo essere consapevoli che i risultati attesi sono limitati dalle approssimazioni fatte. Dobbiamo cioè capire fino a che punto determinate considerazioni pratiche sono valide altrimenti otteniamo risultati sbagliati.

Correnti di bias

Capito che l’uscita è influenzata dalla tensione presente fra i morsetti “+” e “-“ , vogliamo vedere come ridurre questa tensione. Poniamo idealmente il morsetto “+” a massa. Se nel morsetto “-“ non entra corrente allora la sua tensione è calcolabile con la formula (1) del partitore di tensione. In realtà l’amplificatore, per funzionare, ha bisogno di una corrente in ingresso ai due morsetti, detta di polarizzazione o di bias. Per un funzionamento corretto dello stadio differenziale di ingresso le due correnti dovrebbero essere uguali (in modo da amplificare, appunto, solo le differenze), ma in generale non è possibile ottenere una perfetta simmetria. Allora ci si riferisce alla corrente di polarizzazione, o bias, come la media delle due correnti entranti (se fossero uguali, sarebbero proprio uguali alla media!). Se riguardiamo lo schema di Figura 1 e poniamo Vin=0 avremo che anche Vout=0, ma soprattutto abbiamo che la corrente di bias entra direttamente nel morsetto “+” che risulta a massa, mentre nel morsetto “-“ passa dalle resistenze R1 e R2 (che si ritrovano in questo caso ad essere in parallelo) determinando una tensione diversa da zero (la epsilon di prima). Per eliminare questa differenza di tensione, ovvero per eliminare l’effetto delle correnti di polarizzazione, occorre che anche il morsetto “+” sia allo stesso potenziale e quindi si deve inserire in serie al generatore Vin una resistenza Rx=R1//R2. Lo schema che ne risulta è mostrato in Figura 5 dove per semplicità Rx è realizzata proprio come il parallelo di due resistenze di valore pari a R1 e R2.

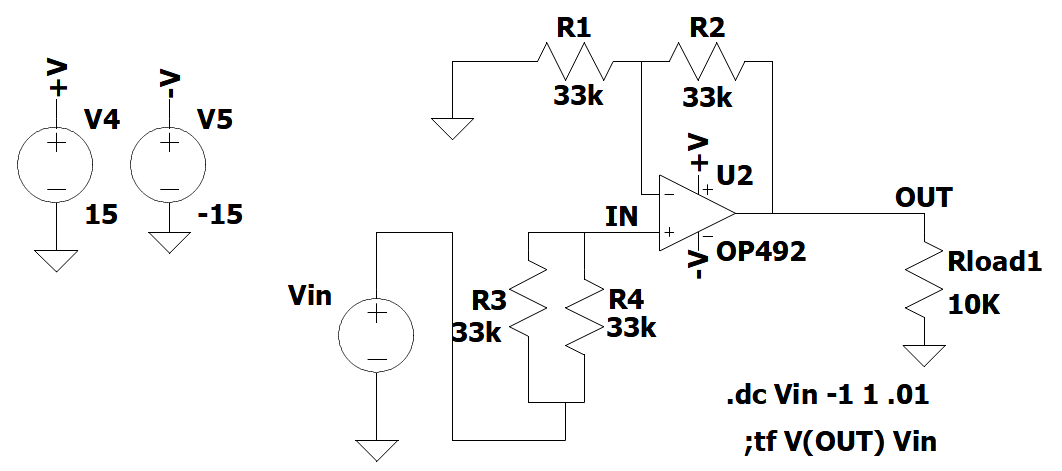
Figura 5

II risultato, visibile in Figura 6, mostra una tensione di uscita in linea con quanto previsto, infatti l’errore in uscita per ingresso nullo si è ridotto a 3.6 mV circa. Questo errore residuo è dovuto al fatto che le due correnti in ingresso all’OpAmp non sono uguali ma presentano una differenza, detta corrente di offset (riportata in genere sui datasheet in valore assoluto, perché non è possibile conoscerne apriori il segno). Per ridurne gli effetti, in quelle applicazioni dove è richiesta una elevata precisione, si usano amplificatori che presentano dei morsetti aggiuntivi dove collegare dei trimmer da regolare fino a quando non si ottiene il risultato voluto.

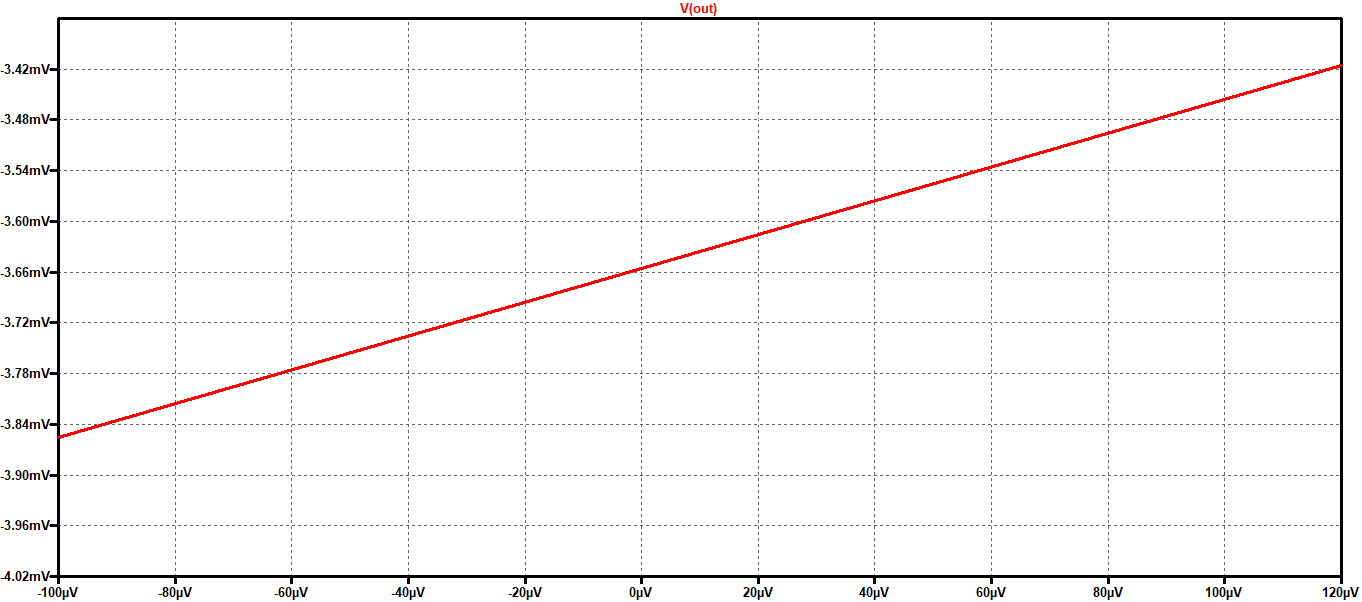
Figura 6

In figura 7 sono riportate le correnti in ingresso (positive se entranti) e, come si vede, sono I(-)= -410 nA, I(+)=-390 nA, per cui Ib=400 nA e Io=20 nA, in linea con i valori presenti sul datasheet. Si noti soprattutto come esse non dipendono dal valore della tensione Vin, essendo caratteristiche dell’OpAmp (definite dai circuiti interni all’integrato).

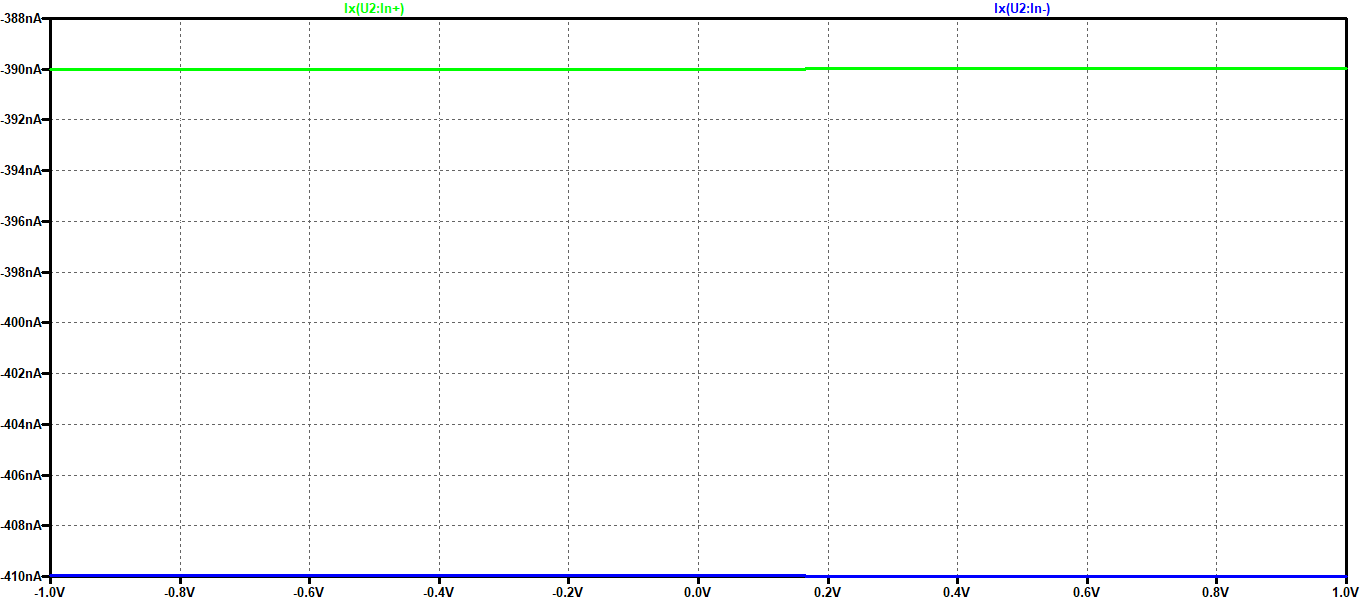
Figura 7

Circuito separatore (Buffer)

Ci si potrebbe chiedere a cosa può servire un circuito che amplifica poco la tensione in ingresso e che presenta tutta una serie di accorgimenti per funzionare. In realtà le peculiarità di questa configurazione sono altre, infatti determinando la caratteristica di trasferimento con il comando:

.tf V(OUT) Vin

si vede che il circuito presenta una elevatissima resistenza di ingresso oltre una bassa di uscita. Questo fa si che il generatore Vin operi “a vuoto” ovvero non sia influenzato dal carico (e nemmeno dalla resistenza in serie Rx) assorbendo una corrente trascurabile e quindi anche in presenza di un generatore reale, la tensione di uscita è proporzionale alla tensione (a vuoto) dell’ingresso.

— Transfer Function —
Transfer_function: 1.99983 transfer
vin#Input_impedance: 3.63203e+010 impedance
output_impedance_at_V(out): 0.0211472 impedance

Da questo punto di vista il circuito non invertente opera come un separatore fra una sorgente non ideale e gli stadi amplificatori a valle. In particolare se sostituiamo a R2 un corto circuito, anche R1 (e quindi Rx) diviene superflua: l’amplificatore avrà guadagno unitario ma servirà a fornire un segnale di potenza adeguata ai circuiti a valle, comportandosi come un generatore ideale di tensione.

Conclusioni

A partire da un circuito in configurazione non invertente abbiamo analizzato alcune limitazioni nelle scelte progettuali dovute a guadagno finito e correnti di bias per arrivare ad utilizzare questa configurazione come circuito separatore, molto utile per interfacciare sensori e circuiti di amplificazione ed elaborazione dei segnali.