Introduzione
Proponiamo un esperimento concettuale che restituisce la famosa relazione di interminazione tempo–energia.
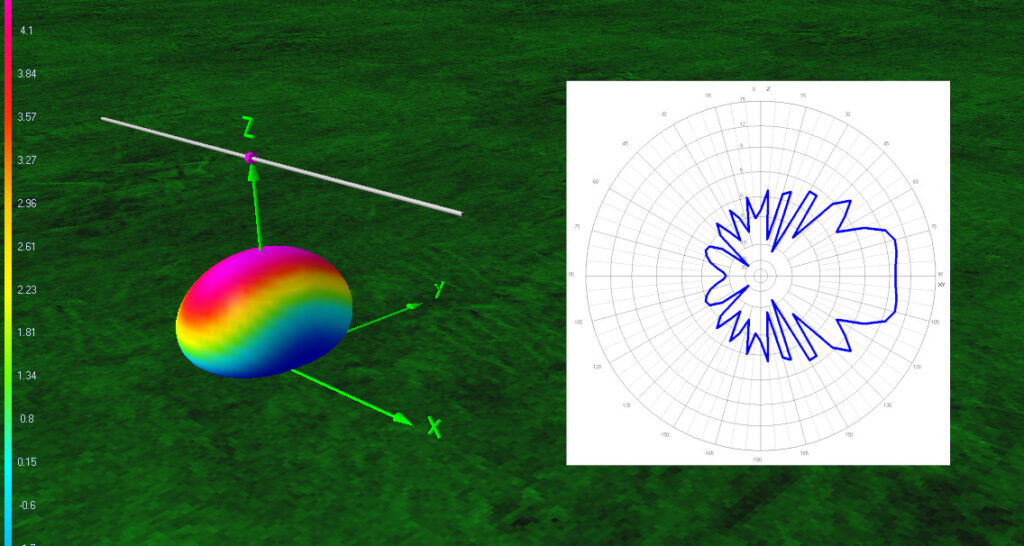
Campo di onda piana emesso da un’antenna
Consideriamo il seguente problema: un’antenna emette un campo elettromagnetico (E,B) tale che
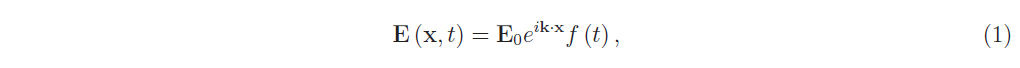
dove: x = (x, y, z) è il vettore posizione del punto dello spazio fisico in cui si valuta il campo; E0
è l’ampiezza complessa; k è il vettore di propagazione dell’onda (assumendo tale vettore costante in direzione e modulo, si ottiene un campo d’onda piana); la grandezza f (t) esprime la dipendenza temporale del campo elettrico. Nel caso particolare di un’oscillazione sinusoidale di durata τ:

come mostrato in fig. 1.
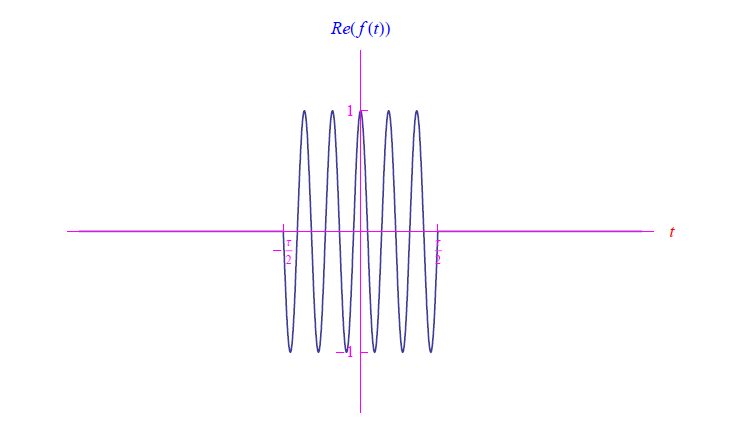
Figura 1: grafico di Re f (t)
Evidentemente
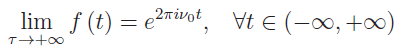
ovvero l’antenna emette un’onda piana monocromatica (i.e. con un’unica frequenza v0). Per un’oscillazione di durata finita ci aspettiamo una dispersione in frequenza, che pu`o essere stimata sottoponendo la funzione f (t) ad analisi di Fourier. Scriviamo lo sviluppo di f (t) in integrale di Fourier:
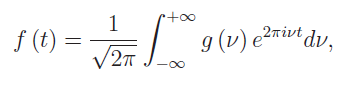
essendo g (v) la densità spettrale, cioè la trasformata di Fourier di f (t)
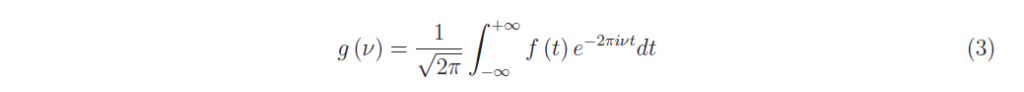
Calcolando l’integrale si ottiene:
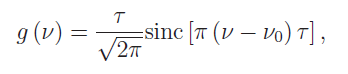
cioè la funzione sinc centrata in v0. E’ più interessante lo spettro di potenza |g (v)|^2 graficato in fig. 2. Si osservi che al crescere indefinito della durata τ, lo spettro di potenza si assottiglia progressivamente per poi tendere a una funzione delta di Dirac centrata in v0 (per una durata τ infinita). Viceversa, la riga spettrale avrà una dispersione in frequenza dell’ordine
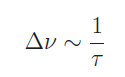
Come è noto, un campo elettromagnetico è costituito da fotoni (il famoso dualismo onda-corpuscolo), e l’energia di singolo fotone è
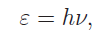
dove h è la costante di Planck. Ne segue
![]()
per cui
![]()
che esprime, come anticipato, la relazione di indeterminazione tempo energia per singolo fotone.
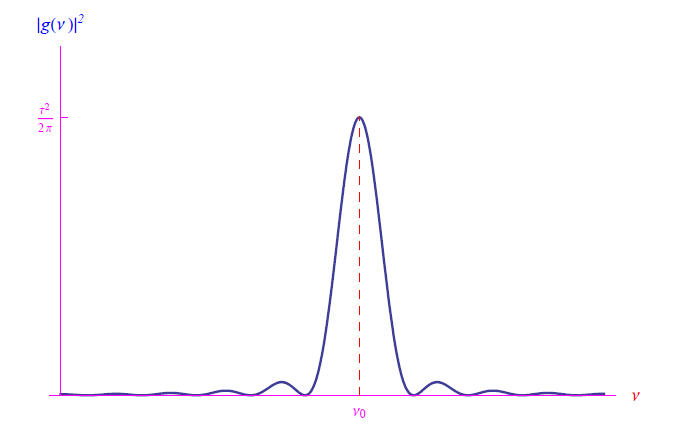
Figura 2: spettro di potenza dell’oscillazione f (t)