Generalmente non è sarebbe possibile effettuare tale operazione poiché il rumore è informazione “degradata”. Vediamo di comprendere, da un punto di vista esclusivamente matematico, la questione delle variabili aleatorie, e quindi del “noise”.
Il Rumore dal punto di vista matematico
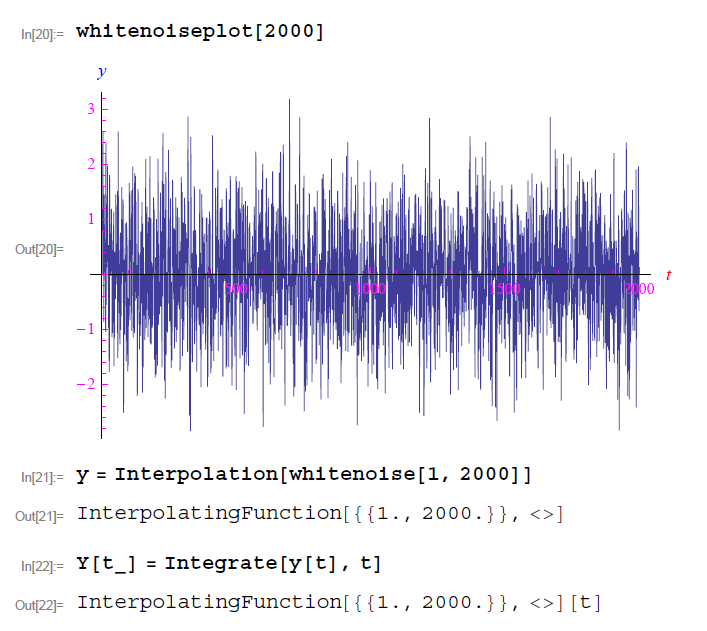
Matematicamente il White Noise (rumore bianco) è una funzione che ha, in ogni punto del suo campo di esistenza, una discontinuità di prima specie. Questo perché i valori assunti nel tempo sono scorrelati al 100%. Ad esempio se y(t) è un White Noise, il valore che tale grandezza assume a un istante y(t+dt) è completamente scorrelato al valore y(t). Ne consegue che non c’è continuità tra y(t) e y(t+dt). La funzione “salta” istantaneamente (dt è un infinitesimo) da un valore all’altro. E questo succede per ogni valore di t. Ecco perché il White Noise ha un andamento così irregolare. Ed è chiaro che non esiste alcuna espressione elementare di tale funzione. Ma non potrebbe comunque esserci perché y(t) è aleatoria, cioè non sappiamo quale valore assumerà in y(t+dt). Possiamo solo conoscere la probabilità che y assuma un dato valore. Il software Mathematica calcola una “istantanea” della y(t), cioè calcola i possibili valori assunti, ed è chiaro che se si ripete nuovamente la simulazione, si ottiene un andamento diverso che riflette l’aleatorietà di y. In ogni caso, proviamo a lavore su una “istantanea”. Abbiamo detto che è una funzione con infiniti “salti” (punti di discontinuità di prima specie) e per Mathematica si tratta di una lista di numeri che possiamo plottare con ListLinePlot. Eseguiamo un’interpolazione: Mathematica forza una qualche combinazione di polinomi in modo da passare per tutte quelle discontinuità, riproducendo una qualche continuità. Quindi possiamo plottare con Plot[]. Ma la cosa più interessante è che possiamo integrare tale funzione, generando un Brown Noise (o processo di Wiener). Siccome la derivata di tale funzione è una funzione con infiniti punti di discontinuità di prima specie (anche se poi Mathematica riesce a “raggirarli” tramite interpolazione), si ottiene che una qualunque primitiva di y(t) è una funzione continua ma non derivabile in alcun punto. Precisamente ogni punto del grafico è un punto angoloso. Segue una curva infinitamente frastagliata. Potrebbe trattarsi anche di un frattale (tipo curva di Koch). Da un punto di vista fisico, invece, si può calcolare la potenza grazie alla varianza. Ma solo se il processo aleatorio è stazionario, anzi, ergodico. E qui si apre un’altra domanda: “Passando a un segnale in propagazione, se un Noise ha potenza, quindi energia, non sta trasportando energia? E quindi informazione?”.
Definire la densità di probabilità
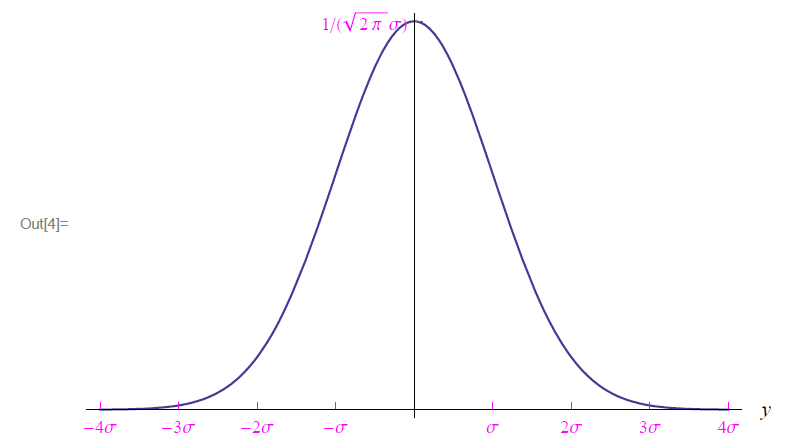
Il problema che ci poniamo ora è come costruire un’assegnata densità di probabilità relativa a una variabile aleatoria y(t). Ricordiamo che la locuzione “densità di probabilità” si riferisce a una funzione continua ρ(y) tale che ρ(y0) dy è la probabilità infinitesima che una misura della variabile y fornisca un valore appartenente all’intervallo [y0, y0 + dy]. Riferiamoci in particolare a una variabile gaussiana i.e. una variabile la cui densità di probabilità è una distribuzione gaussiana di valore medio μ e varianza σ2, che viene invocata dal comando:


Generare numeri reali casuali
Il modo più veloce per generare un White Noise consiste nel creare una lista di numeri reali casuali y1, y2, …, yn. A tale scopo utilizziamo il comando RandomReal[].

Nota: in realtà sono numeri “pseudocasuali”, poiché l’algoritmo che li genera è deterministico. Quindi:
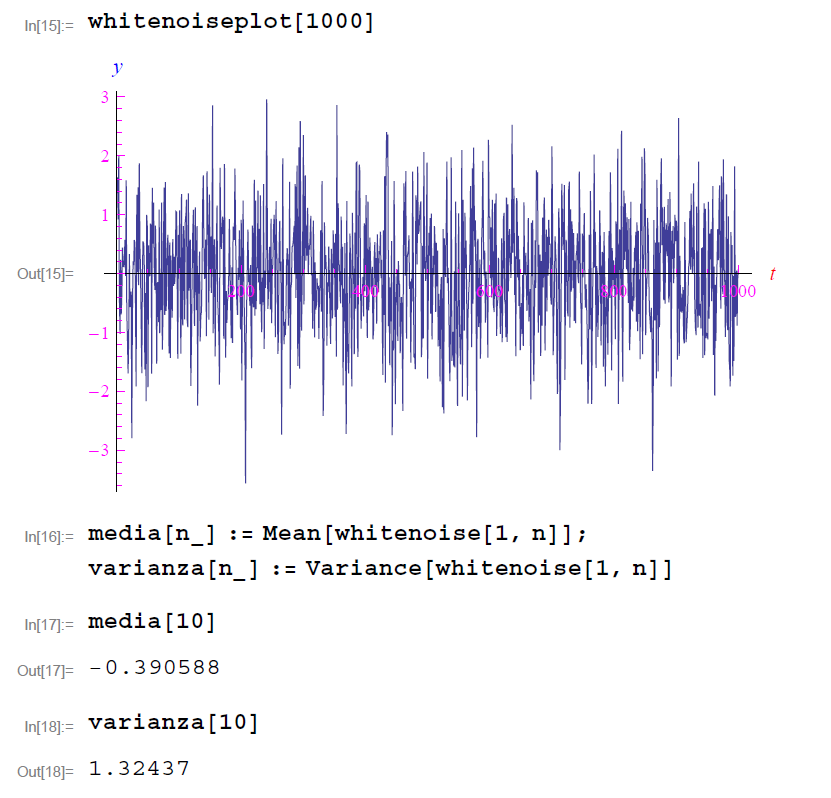
Per il calcolo del valore medio e della varianza, Mathematica dispone dei comandi Mean[] e Variance[]:

In questo modo non abbiamo un controllo sul valore medio e sulla varianza. Ricordiamo che quest’ultima è la potenza media del segnale, e potrebbe essere assegnata a priori. Possiamo generare un White Noise di potenza media assegnata, forzando Mathematica a generare una lista di numeri reali casuali con varianza nota. A tale scopo definiamo la funzione:

Assumendo un valor medio nullo:

Per graficarne l’andamento, definiamo una funzione che ha per argomento l’ordine n della lista definita sopra.

Per n = 1000:
L’approssimazione migliora al crescere di n:

Assumendo n = 2000:
Eseguendo una simulazione con Mathematica, abbiamo provato a trasmettere un segnale di prova sinusoidale a BF in modulazione di ampiezza, utilizzando una portante “rumorosa”, come evidenziato dal seguente grafico:

Altri interessanti articoli su http://www.extrabyte.info/

















