Risolvere le equazioni non è sempre un’operazione facile. Le equazioni lineari di primo o di secondo grado si possono facilmente risolvere con metodi veloci ed elementari. Ma altre tipologie di equazioni (con alto grado oppure o non lineari) risultano oltremodo complicate e la relativa risoluzione potrebbe risultare un’operazione alquanto difficoltosa. Vediamo come la programmazione di un linguaggio di programmazione aiuti in questo senso e come il metodo Montecarlo contribuisca ad arrivare alla determinazione delle soluzioni, anche se non si conoscono le metodologie di risoluzione matematiche. Si può pensare, dunque, di abbandonare momentaneamente i vari metodi di sostituzione, di Cramer, di confronto, di bisezione, di Newton, di Jacobi e Gauss-Seidel, del Gradiente Coniugato e altri per raggiungere, ugualmente, la risoluzione finale.

Primo esempio: passiamo subito al sodo

Molto spesso sui social si vedono dei post di amici che propongono quiz e indovinelli matematici. Il più delle volte si tratta di equazioni complicate, magari di grado superiore a 5. Si supponga di leggere il seguente quesito al fine di risolvere l’equazione:

prevedendo soluzioni intere e reali. Risolvere un’equazione di quinto grado non è poi così semplice. Vediamo come procedere. Abbiamo bisogno di forza bruta e velocità massima. Il metodo Montecarlo, nel nostro caso, si basa sulla generazione di un numero casuale intero e positivo che possa sostituire il valore dell’incognita e calcolare, di conseguenza, l’equazione. Si comprende subito come tale metodologia distolga l’utente dal conoscere i metodi risolutivi necessari. Occorre solo insegnare la tecnica di sostituzione al calcolatore, e il gioco è fatto. Per le prove utilizziamo, ovviamente, il linguaggio C, che risulta il più veloce di tutti gli altri linguaggi di programmazione. Lo scopo, infatti, è quello di generare il più alto numero di valori casuali, che vadano a sostituire le variabili dell’esercizio, nel modo più rapido possibile.

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main() {
     long x,e;
     srand(time(NULL));
     printf("Inizio\n");
     while(1) {
         x=rand();
         e=x*x*x*x*x-2*x*x*x*x-x*x*x+8*x*x-x+8;
         if(e==2875188)
            printf("Valore di X: %ld\n",x);
     }
 }
  

Come si vede, invece di usare la funzione pow(), appartenente alla libreria “math”, l’elevamento è stato effettuato moltiplicando “n” volte il valore della x. L’algoritmo non termina mai perché staziona in un ciclo infinito. Pertanto si deve bloccarlo premendo i tasti <CTRL><C>. Essendo generati dei numeri casuali si potrebbero ripetere le soluzioni già proposti in precedenza, ma questo problema è irrilevante. Purtroppo la funzione rand() genera numeri casuali interi da 0 a RAND_MAX, di solito pari a 32767, ma è possibile raggirare tale “limite”. Come si vede dal risultato, una delle 5 possibili soluzioni che ammette l’equazione è di tipo reale e intera, le altre sono immaginarie.

Secondo esempio: coefficienti negativi

E’ sempre consigliabile prevedere una generazione stocastica di cifre negative. L’algoritmo che segue genera numeri anche negativi, oltre che positivi, e utilizza anche la funzione pow() per effettuare l’elevamento a potenza, ottenendo una codifica più comoda. Si debba risolvere, ad esempio, la seguente equazione:

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>
int main() {
    long x,e;
    srand(time(NULL));
    printf("Inizio\n");
    while(1) {
       x=rand()-16384;
       e=12*pow(x,8)+2*pow(x,7)-5*pow(x,6)-pow(x,5)-2*pow(x,4) pow(x,3)+8*pow(x,2)-x+8;
       if(e==4455338)
            printf("Valore di X: %ld\n",x);
    }
}

Anche questa volta l’equazione prevede una soluzione intera e reala. Risolvere un’equazione di ottavo grado risulta abbastanza complicato. E’ utilizzata la funzione pow() per l’elevamento a potenza. L’esecuzione deve essere sempre bloccata premendo i tasti <CTRL><C>. Anche in questo dato la soluzione viene visualizzata sul monitor.

Terzo esempio: avvicinamento successivo

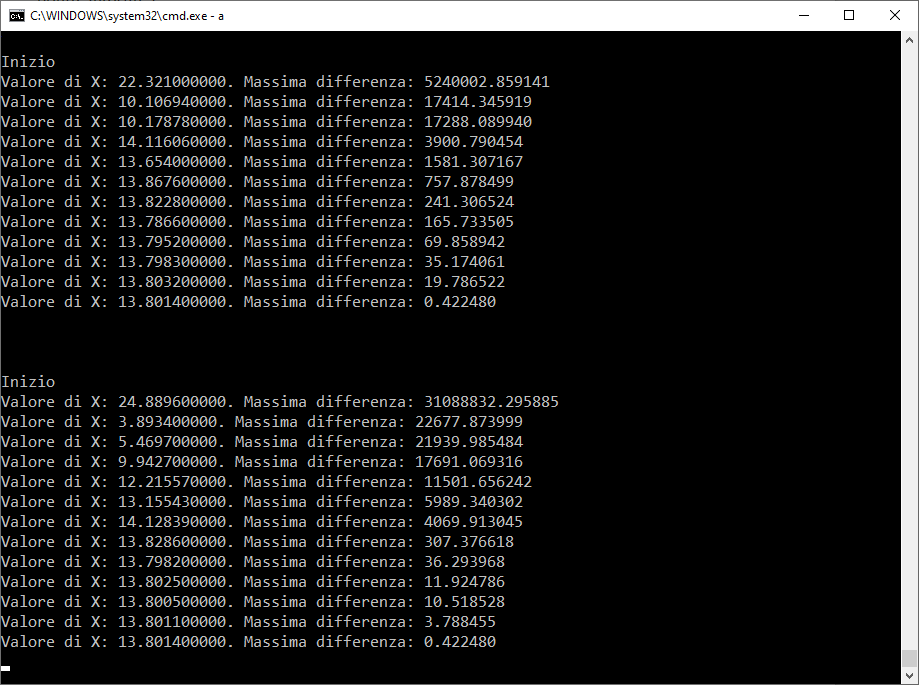
Il terzo esempio è più complesso, prevede radici non intere positive e una visualizzazione progressiva per avvicinamento alla risoluzione finale. Si debba risolvere la seguente equazione:

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>
int main() {
    long ParteIntera,ParteDecimale;
    char st[20];
    double x,e,diff,maxdiff;
    srand(time(NULL));
    printf("Inizio\n");
    maxdiff=99999999.9;
    while(1) {
        ParteIntera=rand()%100;
        ParteDecimale=rand();
        sprintf(st,"%ld.%ld",ParteIntera,ParteDecimale);
        x=atof(st);
        e=pow(2,x)+pow(x,2)+47*pow(x,2);
        diff=fabs(e-23420.3454396);
        if(diff<maxdiff) {
            maxdiff=diff;
            printf("Valore di X:%3.9f. Massima differenza:%f\n",x,maxdiff);
        }
   }
}

Il codice è molto interessante e introduce un primo tentativo di algoritmo genetico, ovviamente estremamente primitivo e non migliorativo. La videata finale fa comprendere come il punto di partenza della ricerca possa essere il più diversificato, data l’aleatorietà dell’approccio, ma il punto finale converge sempre verso la soluzione.