Un MOSFET in stato di conduzione lavora con una efficienza massima, in quanto la tensione Drain-Source è minima, come pure la dissipazione di potenza. Ma se esso lavora in un sistema dinamico, le veloci commutazioni lo relegano in brevissime zone lineari, che ne degradano l’efficienza finale. I progettisti, dunque, oltre che a considerare e analizzare gli aspetti elettrici ed elettronici dei sistemi di potenza, oggi devono avere un nuovo occhio di riguardo per le temperature di esercizio dei diversi componenti elettronici. I nuovi simulatori permettono l’osservazione di questo nuovo parametro.
Le temperature di lavoro sono un dato essenziale da monitorare
L’elettronica di potenza oggi presuppone uno stretto controllo del comportamento termico di un sistema, oltre che delle prestazioni elettriche. Un aspetto impegnativo della progettazione di circuiti di potenza è quello di verificare che il SOA di un MOSFET non venga superato, tenendo sotto controllo le temperature di giunzione. Si può considerare la temperatura di giunzione come la temperatura reale del semiconduttore, invece quella che si misura sulla superficie del componente è leggermente minore per la resistenza termica del contenitore che si oppone al passaggio del calore. Un aumento di temperatura rispetto a quella ambientale indica che esiste una sorgente che trasforma energia in calore. La figura 1 mostra uno schema elettrico generico di un riscaldatore a resistenza di potenza. Il suo funzionamento è il seguente:
- per i primi 60 secondi, la resistenza è fredda;
- per le successive 30 volte, a intermittenza, la resistenza si accende per 25 secondi e si spegne per 5 secondi;
- dopo tale ciclo, il circuito si spegne definitivamente.
Il circuito di esempio funziona a corrente continua ed è formato dai seguenti elementi:
- V2: generatore di segnale per il pilotaggio del MOSFET, secondo le specifiche elencate prima;
- R1: resistenza riscaldatrice di potenza di 4 Ohm. Quando è percorsa da corrente, la sua dissipazione arriva a circa 2300 W;
- U1: MOSFET in grado di sopportare le tensioni e le correnti richieste. Nell’esempio, in conduzione esso dissipa circa 4 W;
- V1: generatore del circuito, con tensione di 96 V;
- U2: dissipatore di calore.
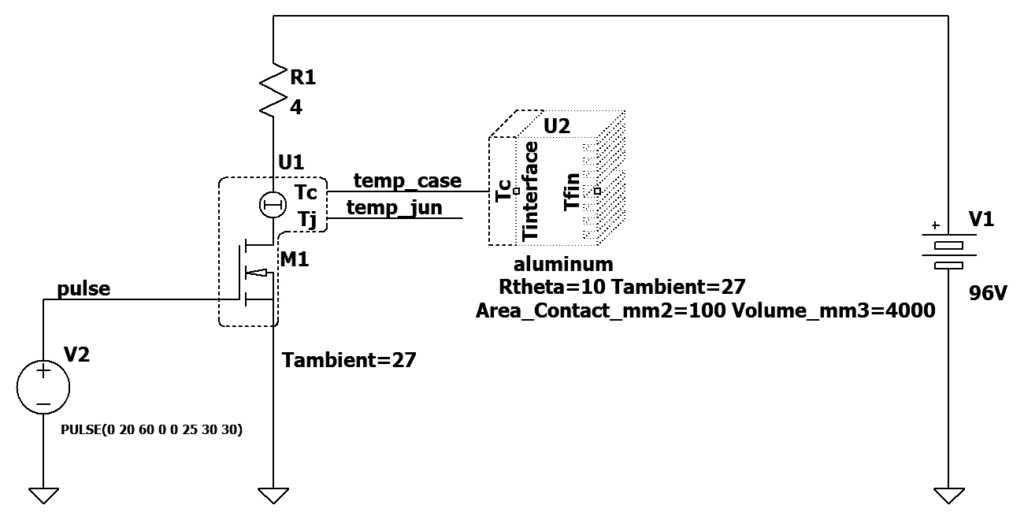
Figura 1: lo schema elettrico di principio di riscaldatore a resistenza intermittente
Il dissipatore di calore, utilizzando i modelli SOAtherm dei simulatore, può essere programmato a piacimento, ed è caratterizzato dai seguenti dati:
- materiale: alluminio;
- coefficiente Rtheta: 10. Quest’ultimo descrive la resistenza termica del dissipatore di calore, espresso in ˚C/W;
- temperatura di ambiente: 27 °C;
- area di contatto con il componente: 100 mm^2;
- volume: 4000 mm^3.
E’ interessante, a questo punto, eseguire una simulazione per controllare i risultati elettrici e termici, mostrati nei grafici di figura 2. La bontà dei dati dipende, in massima parte, dalla qualità dei modelli dei componenti elettronici. In ogni caso, il progettista rammenti che gli esiti finali reali contempleranno molte variabili che un normale simulatore elettronico non può prevedere. Il grafico contiene le seguenti tracce, tutte nel dominio del tempo, partendo dall’alto:
- V(pulse): il segnale che attiva e disattiva il gate del MOSFET;
- I(R1): la corrente che attraversa la resistenza riscaldatrice di potenza;
- V(temp_case): la temperatura del contenitore del MOSFET;
- V(temp_jun): la temperatura di giunzione del MOSFET.
Si noti, altresì, che il simulatore fornisce la misura delle temperature espresse in Volt, ma esse sono a tutti gli effetti delle misure termiche, espressi in gradi Celsius. La temperatura sale per i primi 950 secondi, benché il pilotaggio della resistenza di potenza sia intermittente, per via della inerzia del sistema. A fine ciclo, poi, le temperature raggiungono uno stato di equilibrio (temperatura d’ambiente) dopo circa 1 ora dall’inizio del ciclo e dopo 44 minuti dopo l’ultima attivazione della resistenza. Quasi tutti i sistemi elettronici di potenza richiedono un elevato scambio termico tra i componenti e l’ambiente circostante, al fine di evitare la loro distruzione a causa delle alte temperature.
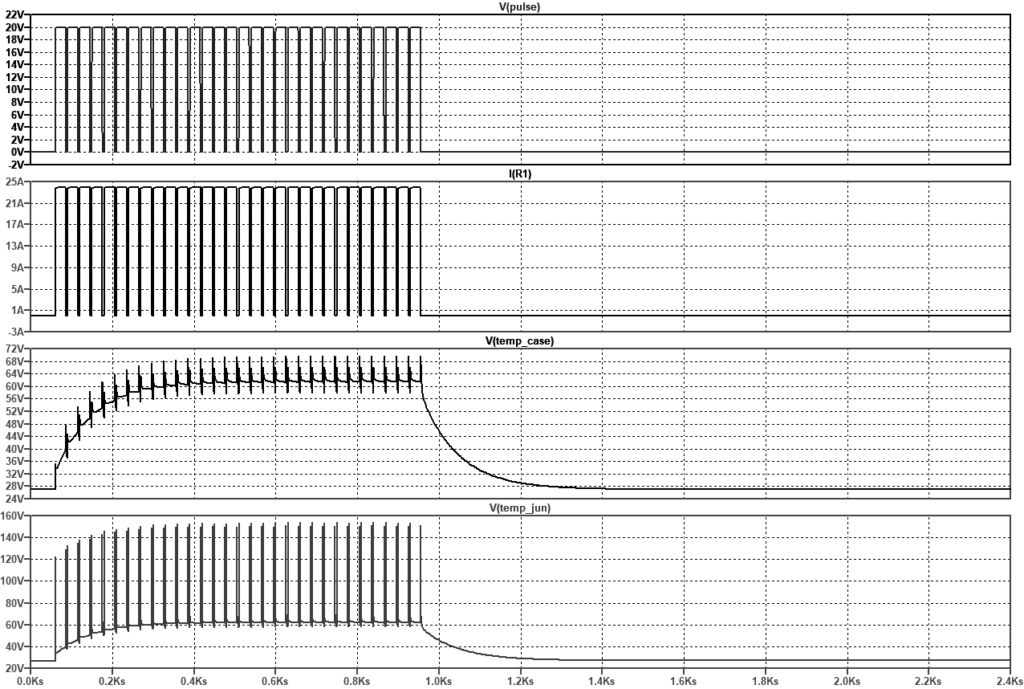
Figura 2: la simulazione del sistema con la visualizzazione della temperatura del contenitore e di giunzione del MOSFET
Il dissipatore deve essere, ovviamente, di metallo. Esistono ottimi materiali che hanno coefficienti termici altissimi. La seguente tabella mostra le conducibilità termiche di alcuni materiali, a 20° C, espressi in W/mK:
| Materiale | Conducibilità termica a 20° C (W/m*K) |
| Argento | 407 W/m*K |
| Rame | 386 W/m*K |
| Oro | 318 W/m*K |
| Alluminio | 204 W/m*K |
| Nichel | 91,2 W/m*K |
| Ferro | 80,6 W/m*K |
Come si può vedere, l’argento è il metallo con la conducibilità termica più alta, seguito dal rame e dall’oro. Ma non si può pretendere di acquistare un dissipatore in oro o in argento, per ovvi motivi. Tale parametro indica quanto calore conduce un materiale. Inoltre quelli caratterizzati da una conducibilità termica alta conducono il calore più velocemente dei materiali con una conducibilità termica bassa. Lo stesso sistema utilizzante gli stessi componenti elettronici ma con dissipatori di alluminio e di rame, producono una risposta di temperatura leggermente differente (vedi in figura 3). Nella fattispecie, con l’alluminio il MOSFET riesce a raffreddare meno, raggiungendo un picco di 182.5° C contro i 175.5° C, ben 7 gradi di differenza. In altre parole, il dissipatore di rame riesce a mantenere più basse le temperature dei componenti.
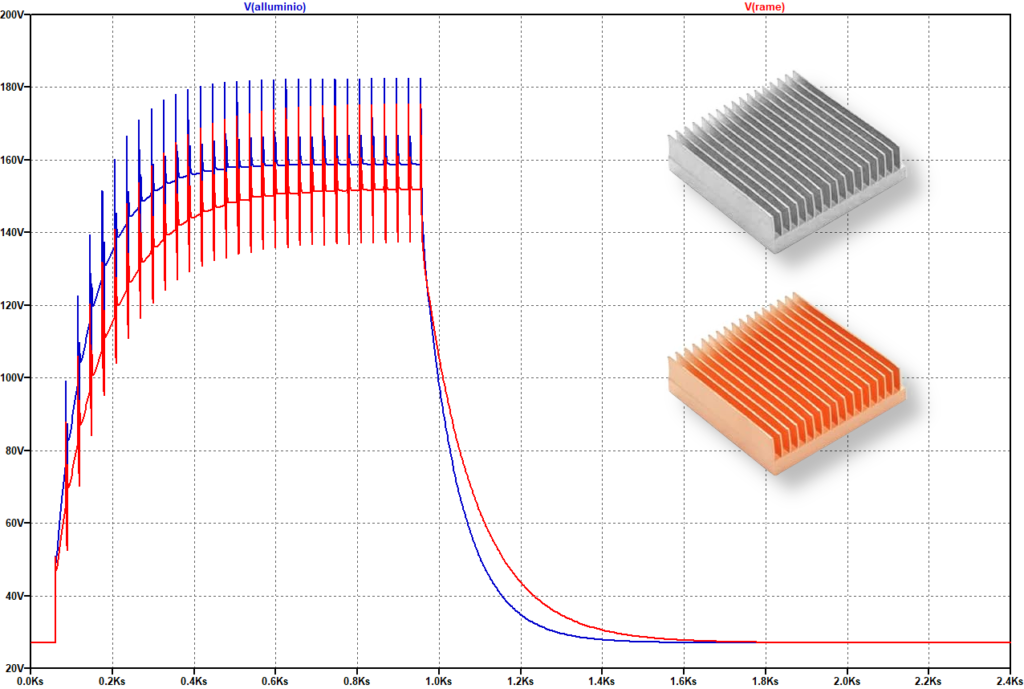
Figura 3: il rame consente una dissipazione termica più efficiente rispetto all’alluminio
Simulazione fisica
Volendo accostare i risultati elettrici eseguiti prima a quelli prodotti con una simulazione fisica, la caratterizzazione del sistema è un tantino più complicata, in quanto sono necessari molti parametri aggiuntivi. La figura 4 mostra il risultato termico finale del transitorio di un sistema statico che alimenta, in modo continuativo, un carico resistivo con un MOSFET. In dettaglio, i seguenti dati caratterizzano il circuito elettrico:
- resistenza del carico: 4 ohm;
- modalità di alimentazione del carico: continuativa;
- corrente sul carico: 24 A;
- potenza dissipata dal carico: 2300 W;
- corrente sul MOSFET: 24 A;
- tensione Drain-Source 135 mV;
- potenza dissipata dal MOSFET: 3.24 W;
- Rds(ON) calcolata: 0.0056 ohm (5.6 milliOhm).
Il circuito termico, invece, è caratterizzato dai seguenti dati:
- materiale del dissipatore: alluminio;
- il dissipatore nell’esempio è un semplice blocco di alluminio, a forma di parallelepipedo, senza alette di raffreddamento, per semplificare i calcoli;
- conduttività termica dell’alluminio utilizzato: 200 mW / mm * °C;
- rTheta: 10;
- temperatura ambiente: 27° C;
- coefficiente di convezione: 0.05 mW / mm^2 * °C;
- area di contatto tra il dissipatore e il MOSFET: 100 mm^2;
- volume del dissipatore: 4000 mm^3;
- misure del dissipatore: 20 mm x 20 mm x 10 mm;
- potenza dissipata dal MOSFET: 3.24 W.
La simulazione fornisce, dopo il transitorio temporale e al raggiungimento dell’equilibrio termico (che avviene dopo circa 10 minuti dall’inizio del funzionamento), la temperatura di circa 60° sul dissipatore. Naturalmente il simulatore fisico approfondisce la questione più in profondità, fornendo anche i gradienti termici degli oggetti e indicando i punti di massima e di minima temperatura. Nel dettaglio, la temperatura massima raggiunta è di 62.08° C (in corrispondenza dell’area di contatto tra MOSFET e dissipatore) mentre quella minima è di 61.5° C, (in corrispondenza delle zone periferiche del dissipatore).
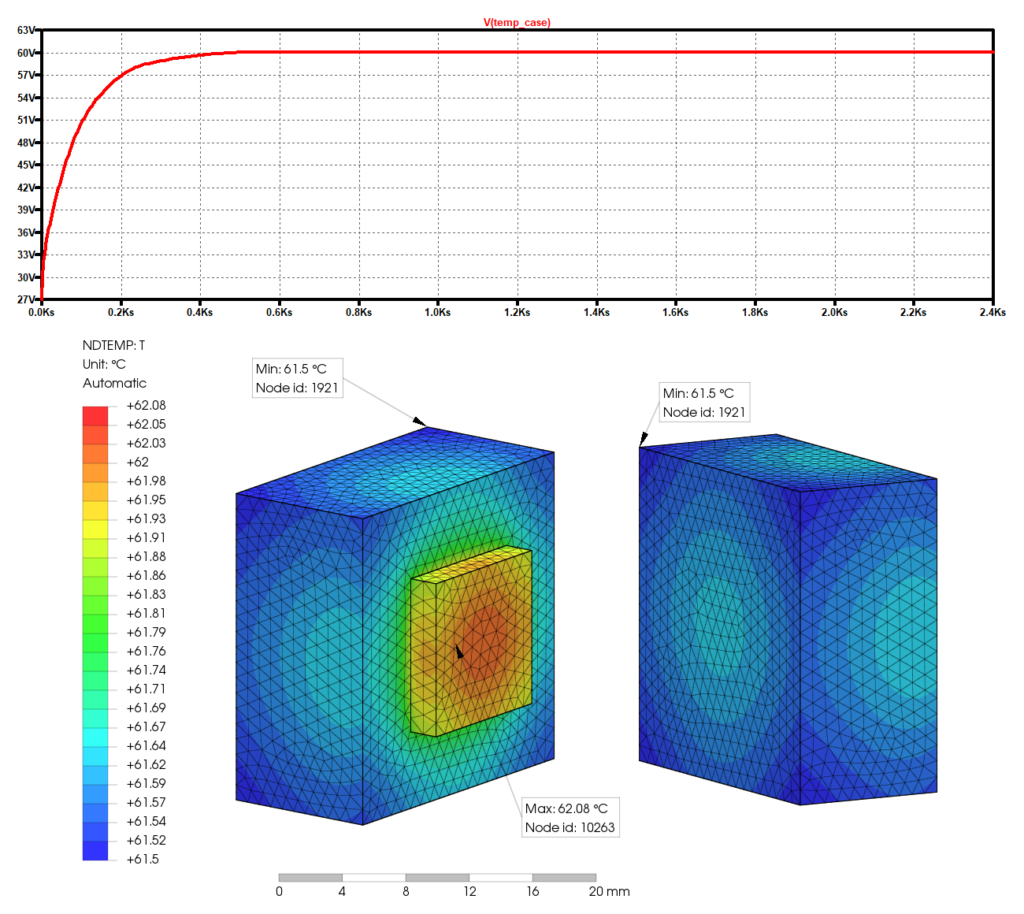
Figura 4: la simulazione termica di un sistema con MOSFET
Cambiando le condizioni operative ed elettriche (impedenza del carico, tensione di alimentazione, tipo di MOSFET, dimensioni e materiale del dissipatore, eccetera) si modificano, di conseguenza, tutti i risultati finali.
Conclusioni
I modelli di simulazione termica sono oggi sempre più numerosi. Spesso le simulazioni dei comportamenti dei sistemi sono lente, poiché i software devono prevedere migliaia di calcoli ed equazioni matematiche. Il regime statico è quello più conveniente per il funzionamento dei MOSFET mentre in regime dinamico (segnale rettangolare, PWM, ecc), la loro efficienza può diminuire a causa delle perdite di commutazione. Ed è proprio in questo caso che i progettisti devono prestare la loro massima attenzione e le simulazioni termiche possono essere di grande aiuto per determinare una risposta di massima al funzionamento dei sistemi di potenza.