Qualsiasi comportamento in natura, non è escluso nemmeno quello elettronico, è regolato da leggi matematiche, formule ed equazioni. Anche la carica e la scarica di un condensatore segue questa regola. L’articolo mostra come caratterizzare con TuringBot la curva di carica di un elemento capacitivo di un determinato valore, preceduto dal relativo resistore di limitazione della corrente.

La regressione simbolica con TuringBot

Si tratta di un potente software, molto recente, scaricabile all’indirizzo https://turingbotsoftware.com/, che utilizza la regressione simbolica come metodo per scoprire formule matematiche dai dati, senza preoccuparsi del loro formato finale. Dato un insieme di variabili di input x1, x2, x3, ecc. e una variabile di destinazione y, esso troverà diverse soluzioni “f” tali che y=f (x1, x2, x3,…). Le spiegazioni del suo utilizzo possono essere trovate sul sito ufficiale del programma.

Il circuito elettrico

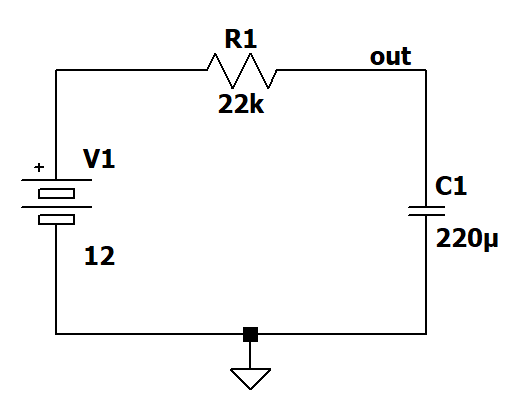
Come si può vedere nella figura seguente, il circuito elettrico utilizzato è un classico ed è composto da un resistore e da un condensatore. In questo esempio i relativi valori sono i seguenti:

• V1: generatore di tensione continua di 12 V;
• R1: resistore di limitazione di corrente di 22 kOhm;
• C1: condensatore elettrolitico di 220 microFarad.

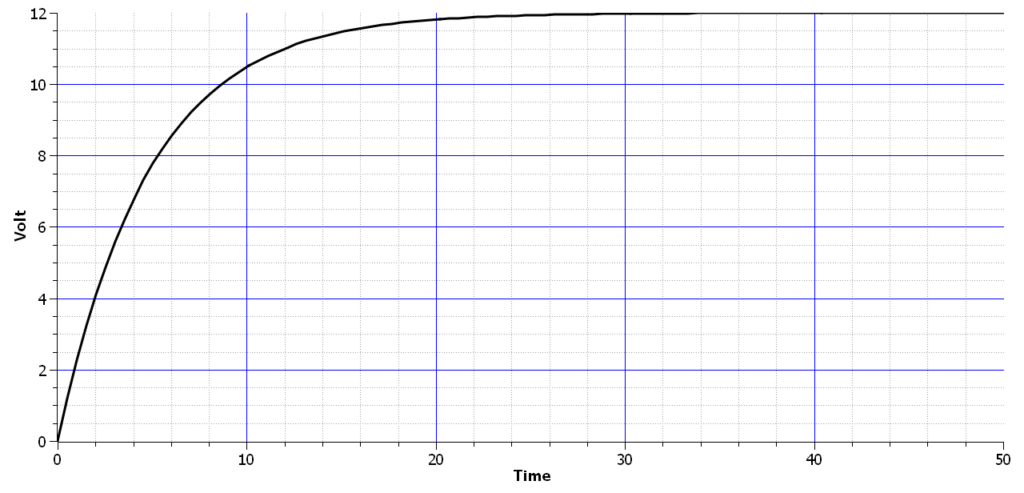
L’attivazione del circuito caricherà il condensatore C1 in un tempo pari a 5 volte la costante di tempo. Il seguente grafico mostra la tensione ai capi del condensatore che, pian piano, si carica sempre di più, attraverso un andamento non lineare ma esponenziale.

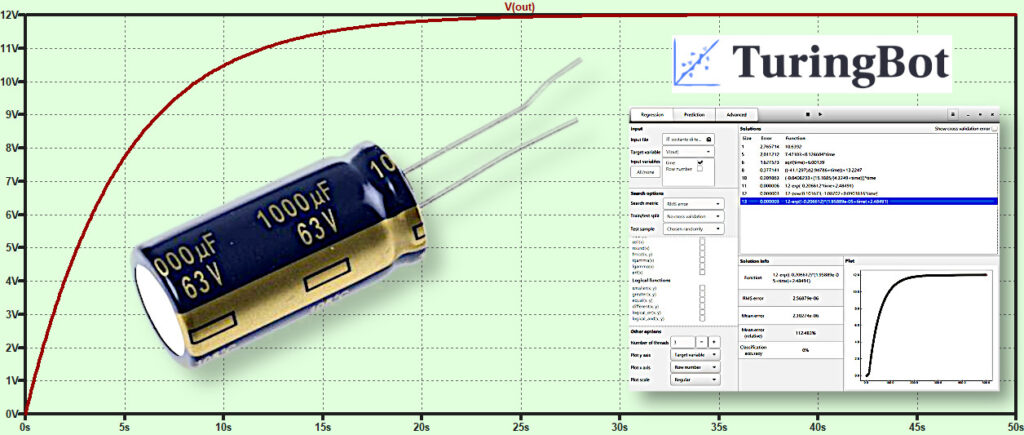
Vogliamo adesso caratterizzare tale comportamento del circuito, alla ricerca di una “probabile” legge matematica che lega il funzionamento dei due componenti.

Creazione di un dataset di valori

La prima operazione da compiere è quella della creazione di una tabella, nel formato (x,y), che raccolga i dati della tensione ai capi del condensatore, nei vari istanti di tempo, compresi tra 0 secondi e 50 secondi. Tale misurazione potrebbe essere anche effettuata manualmente. Si consiglia di approntare una grande quantità di campioni. Il nostro esempio prevede la presenza di ben 500 misure, nel seguente formato:

time V(out)
0.000000000000000e+000, 0.000000e+000
9.999999717180685e-010, 2.479339e-009
1.999999943436137e-009, 4.958677e-009
1.436158342804208e-002, 3.555368e-002
2.872316485608422e-002, 7.100279e-002
4.308474628412636e-002, 1.063473e-001
5.744632771216850e-002, 1.415873e-001
7.180790914021064e-002, 1.767227e-001
8.616949056825277e-002, 2.117536e-001
1.005310719962949e-001, 2.466798e-001
……………………………..
……………………………..
……………………………..
……………………………..
……………………………..
4.986703107252818e+001, 1.199960e+001
4.996943107253158e+001, 1.199961e+001
4.999993107253259e+001, 1.199961e+001
5.000000000000000e+001, 1.199961e+001

Curve Fitting con TuringBot

Siamo pronti, adesso, ad aprire il file di dati precedente creato, con il programma TuringBot. Si impostino le funzioni di ricerca desiderate e, in questo caso, si consiglia di adottare la seguente configurazione:

• addizione;
• moltiplicazione;
• divisione;
• seno(x);
• exp(x);
• log(x);
• sqrt(x);
• pow(x,y);
• abs(x);
• floor(x).

Dopo aver avviato la ricerca, il programma rintraccia diverse soluzioni di formule che possano riprodurre i dati inseriti, con un minore errore possibile. La maggior parte delle volte il software riesce nel suo intento. Dopo alcuni minuti è possibile osservare a video le equazioni scoperte. Ovviamente deve essere considerata quella con il minore errore possibile. La procedura affina sempre di più la precisione dei calcoli, pertanto è sempre consigliabile dedicare molto tempo della CPU per ricerca migliore.

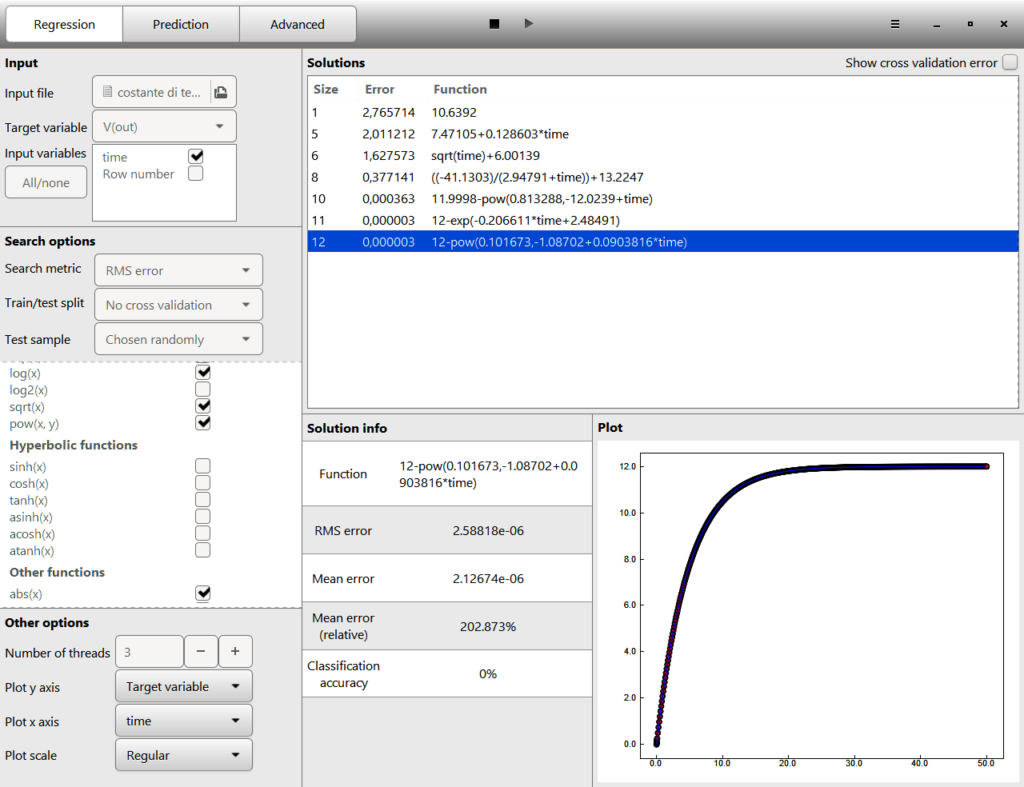
Equazione finale

Il software, dopo circa un’ora di ricerca, ha prodotto la seguente migliore formula:

12-pow(0.101673,-1.08702+0.0903816*time)

corrispondente alla seguente rappresentazione canonica:

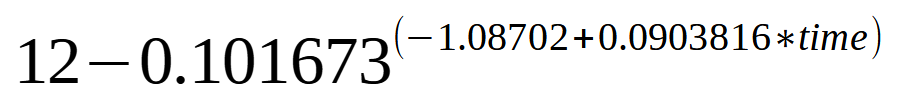
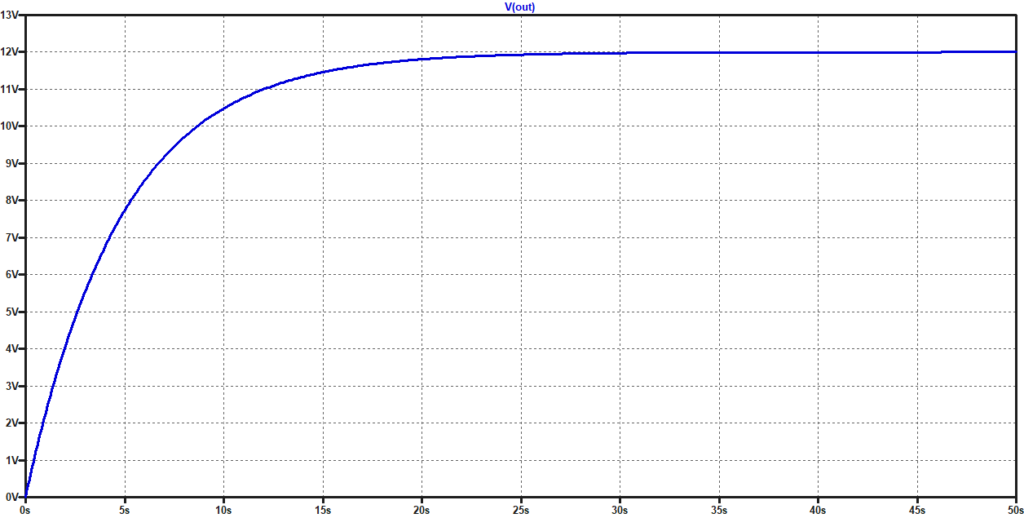
Una sua verifica con qualunque programma di tracciamento grafici confermerà la bontà della soluzione trovata da TuringBot: