Gli Amplificatori Operazionali oltre amplificare segnali, cioè fornire una tensione in uscita proporzionale ad un segnale in ingresso, possono utilizzare i circuiti esterni per realizzare delle vere e proprie “operazioni” matematiche sui segnali, da cui il nome.
Negli articoli precedenti abbiamo analizzato gli OpAmp come “amplificatori”, ovvero come circuiti integrati che presentano un comportamento “quasi” ideale (alta impedenza di ingresso, impedenza di uscita trascurabile e banda passante elevata) con un guadagno determinato dal circuito esterno di retroazione. Ma perché si dice “operazionale”? Che “operazioni” si possono fare?
In tutti i circuiti presentati abbiamo sempre utilizzato solo resistenze ed abbiamo verificato che i legami ingresso-uscita sono di tipo “statico”, cioè l’uscita è proporzionale ai segnali in ingresso.
Per ottenere legami più “dinamici”, dove l’uscita è funzione dell’evoluzione temporale dell’ingresso occorre usare componenti come i condensatori in cui la corrente è proporzionale alla variazione della tensione ai capi del dispositivo.
Matematicamente avremo che la tensione ic è proporzionale alla derivata della tensione vc tramite il valore di capacità:
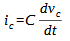
Il circuito integratore ideale di Miller
Utilizzando un condensatore in retroazione al posto di R0, come nel circuito di Figura 1 avremo:
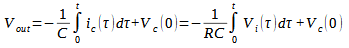
cioè l’uscita è proporzionale all’integrale del segnale di ingresso più il valore iniziale di tensione presente ai capi del condensatore, quindi questo circuito consente di determinare l’integrale del segnale in ingresso.
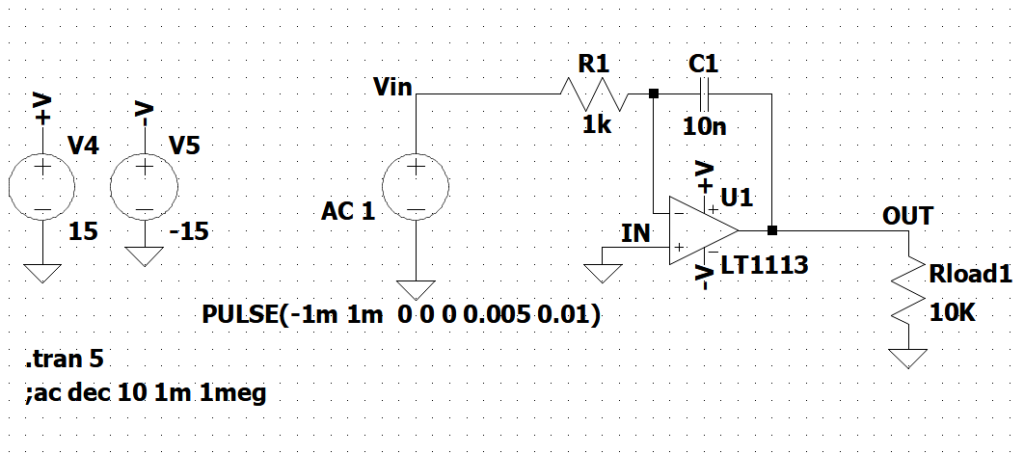
Figura 1: Integratore di Miller
Notiamo subito che questo circuito può operare solo con segnali variabili nel tempo. Se, infatti, l’ingresso è costante l’uscita è una retta che prima o poi porterà in saturazione l’amplificatore.
Questo circuito, però, non può proprio funzionare nella realtà, perché gli OpAmp presentano una tensione (costante) di offset in ingresso e pertanto l’uscita si porterà ad un valore prossimo alla saturazione. Possiamo vedere questo effetto nelle successive figure in cui sono mostrati, rispettivamente, l’uscita quando l’ingresso è una sinusoide ( si vede che è sovrapposta alla costante dovuta all’offset perché presenta un valore medio diverso da zero) ed infine ad un segnale a gradino: l’ingresso è un’onda quadra a valore medio nullo che varia da -1m a 1mV con periodo 10 ms (100 Hz), l’uscita è un dente di sega sovrapposto ad una retta che poi raggiunge il valore di saturazione dipendente dalla tensione di offset.
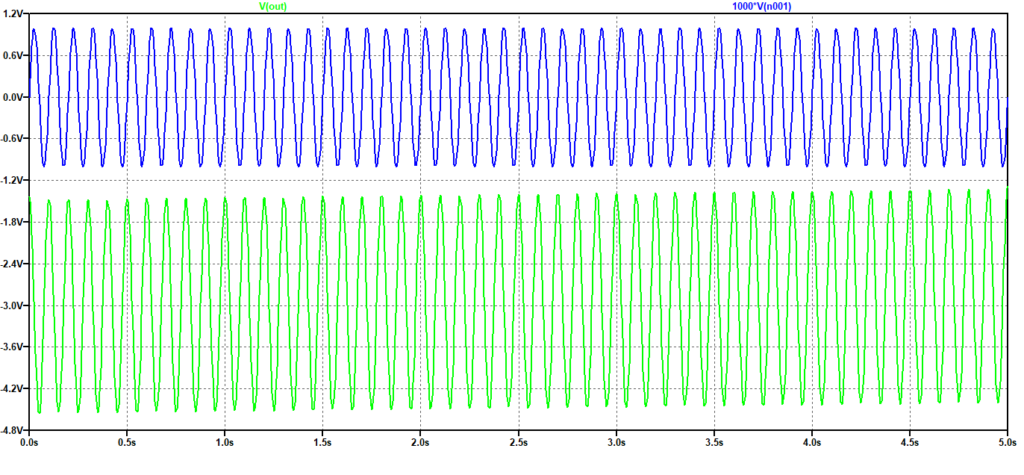
Figura 2: Integrale di una sinusoide
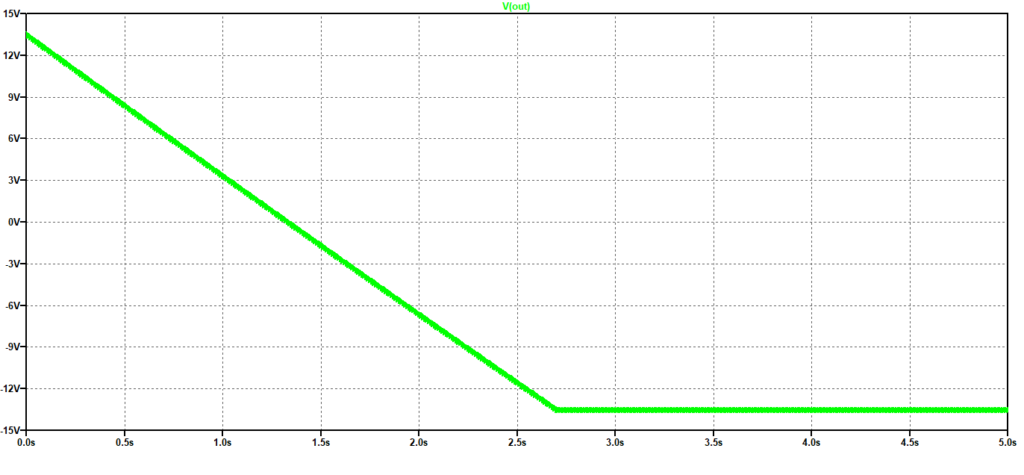
Figura 3: Integrale di un segnale costante a tratti (onda quadra)
Il circuito integratore “reale”
Una soluzione a questo problema consiste nel fornire un percorso alla corrente continua dovuta alla tensione di offset: mettendo in parallelo al condensatore una resistenza, si ha che la componente continua della tensione Vout è determinata dalla rete resistiva e così scompaiono gli effetti di offset. Il circuito è mostrato in ed è indicato in letteratura come integratore “reale” anche se, come vedremo, per raggiungere i migliori risultati serviranno accorgimenti raramente riportati sui libri.
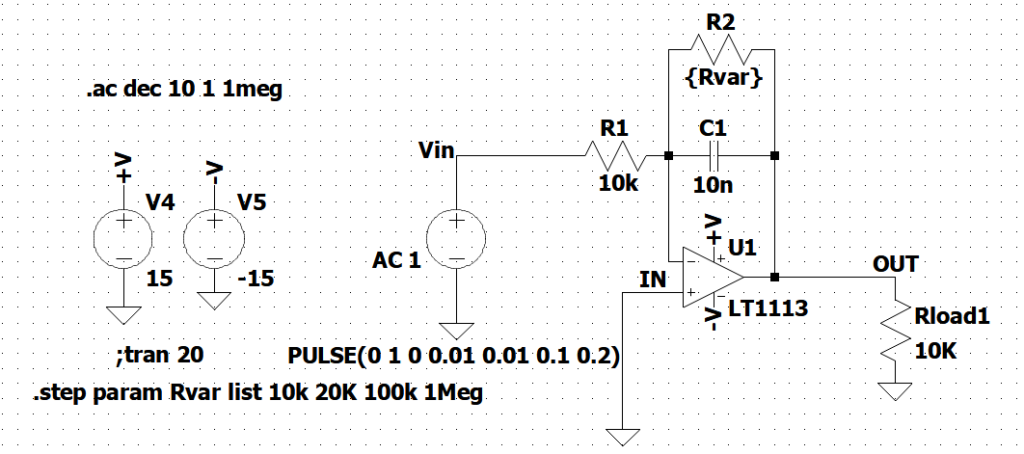
Figura 4: Circuito passa basso usato come integratore
In realtà, come si può vedere dalla risposta in frequenza, riportata in Figura 5 al variare della resistenza R2, il circuito si comporta come un filtro passa basso. Di fatto l’integratore funziona solo con segnali variabili, ma almeno è realizzabile e non risente dell’influenza della tensione di offset.
Mediante una simulazione parametrica (si assegna il valore {Rvar} al resistore e si usa il comando .step param Rvar list 10k 20K 100k 1Meg per calcolare la risposta con i diversi valori) si determina il valore migliore per la resistenza R2 tale da ridurre il più possibile la banda passante ed ottenere un comportamento il più possibile prossimo ad un integratore.
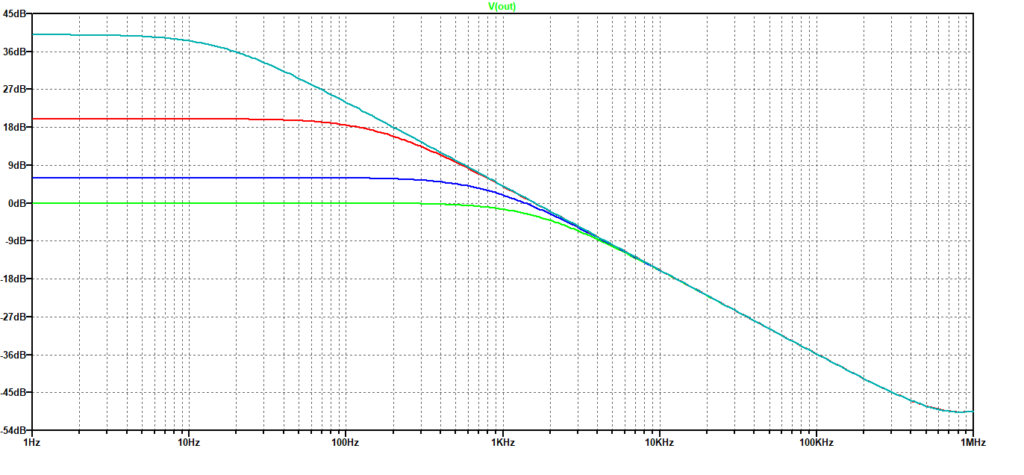
Figura 5: Risposta armonica dell’integratore “reale”
Il valore di R2 ottimale per ridurre la banda è molto elevato e determina, per contro, anche un indesiderato aumento del guadagno in continua.
Notiamo come l’uso della simulazione ci consente di analizzare e dimensionare il circuito senza ricorrere a formule e calcoli complicati.
Integratore T-shunt
Ovviamente la bontà di un circuito è legata all’applicazione e se i segnali da integrare hanno un frequenze superiori alla banda passante del circuito va bene così, ma se non vogliamo limitazioni e cerchiamo prestazioni più vicine ad un comportamento ideale, con banda prossima allo zero senza amplificazioni eccessive allora si devono effettuare delle modifiche al circuito fornendo una via ulteriore verso massa ai segnali variabili.
Dividendo la resistenza R2 in due parti uguali si può inserire una capacità di valore sufficientemente elevato che drena verso massa le componenti variabili. Il circuito è mostrato in Figura 6 e la relativa risposta in frequenza, in Figura 7.

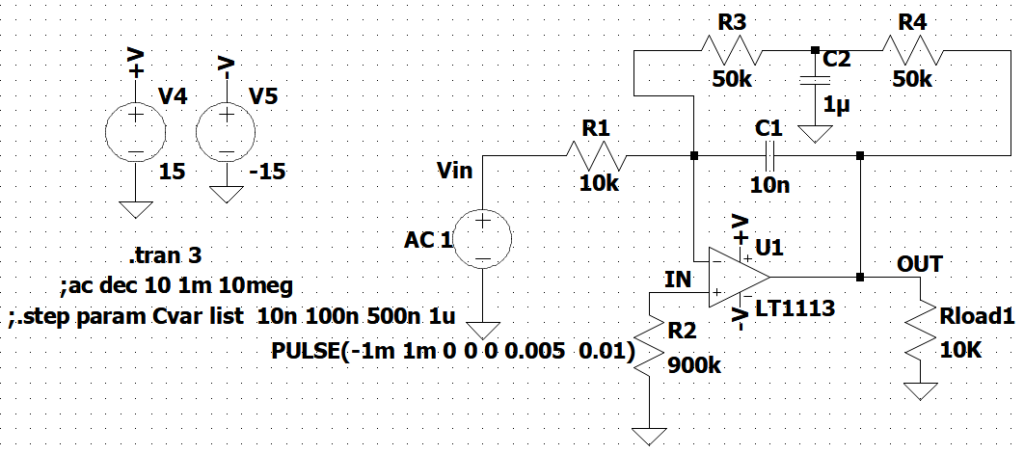
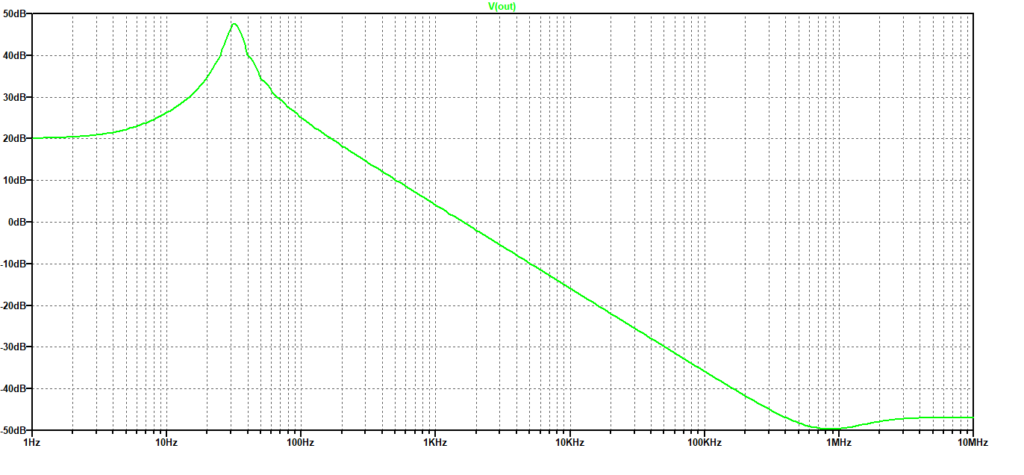
Come è evidente il circuito si comporta da integratore già da 100 Hz, al contrario di quanto si vede in curva in colore rosso, dove si ha un filtro passa basso con frequenza di taglio di circa 200Hz e comportamento da integratore a partire da 1 Khz.
Come esempio del funzionamento da integratore di questo circuito si riporta la risposta ad un’onda quadra a 100Hz a media nulla.
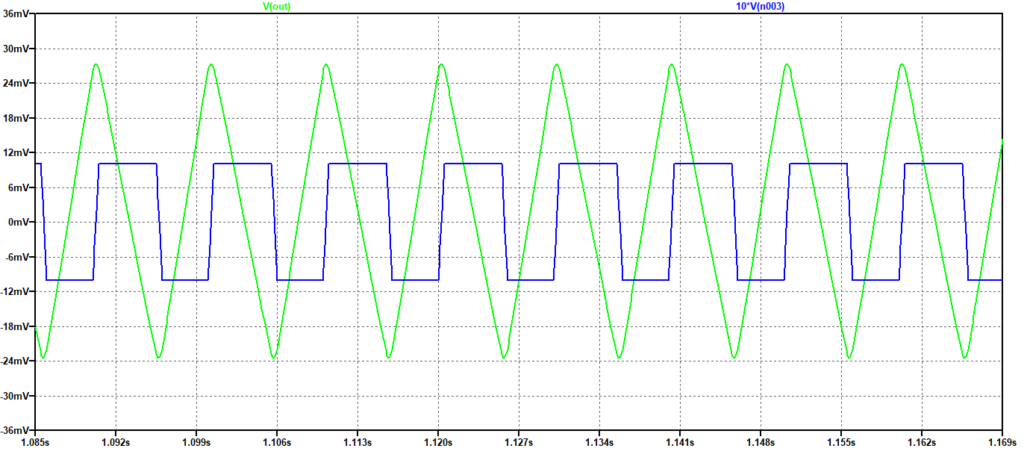
Figura 8: Risposta dell’integratore T-shunt ad un’onda quadra a 100 Hz
Conclusioni
In questo articolo abbiamo utilizzato un Amplificatore Operazionale per realizzare dei circuiti che eseguono operazioni matematiche, come l’integrazione, sui segnali in ingresso. In particolare abbiamo visto come non sia possibile realizzare un integratore ideale ed analizzato diverse soluzioni per approssimarne il funzionamento mostrando i limiti e le condizioni per cui l’approssimazione è valida.

















