Gli Amplificatori Operazionali sono circuiti integrati che normalmente presentano in uscita un segnale (una tensione) proporzionale al valore applicato in ingresso. In genere l’uscita è maggiore dell’ingresso, da cui il nome di “amplificatore”, ma per segnali variabili nel tempo questa amplificazione non può essere costante a tutte le frequenze a causa della presenza di piccolissime capacità dovute alla struttura fisica dei transistor integrati nel circuito (siano essi BJT o MOSFET fa poca differenza). Come spiegato nella parte 1 oltre una certa frequenza il segnale in uscita è addirittura attenuato, ma sempre in modo proporzionale all’ingresso.

Per avere un segnale in uscita proporzionale al valore in ingresso il circuito deve essere “lineare” ma l’amplificatore operazionale è costituito da tanti componenti non lineari che sono polarizzati per funzionare intorno ad un punto di lavoro. Se le variazioni sono “piccole” allora il legame ingresso-uscita è rappresentato da una costante di proporzionalità (che, come detto, dipende dalla frequenza del segnale), ma per “grandi” variazioni può accadere che le non linearità presenti nel circuito rendano l’uscita non più proporzionale all’ingresso ed il segnale risulta “distorto”. Il modello di funzionamento utilizzato finora non tiene in conto, inoltre, di un altro aspetto e cioè il tempo di propagazione del segnale dall’ingresso all’uscita: abbiamo sempre considerato la risposta come un fenomeno istantaneo ma per segnali molto “veloci” (ovvero a frequenza “molto” elevata) questa approssimazione non risulta più valida.

Come capire cosa vuol dire “grandi” e, soprattutto, “veloci” variazioni?

I modelli tipici degli amplificatori sono detti a “piccolo segnale” perché le variazioni di tensione e corrente sono di qualche ordine di grandezza inferiori al punto di lavoro del dispositivo (le tensioni e le correnti continue circolanti nel circuito integrato che garantiscono il funzionamento desiderato). Si chiamano, allora, “grandi” segnali quelli che provocano in uscita variazioni su tutto l’intervallo di tensioni ammissibili (detto anche output swing).

Per capire, invece, quando un segnale è da considerarsi “veloce” dobbiamo pensare al tempo che impiegano i dispositivi all’interno dell’OpAmp per trasferire il segnale in uscita. Oltre una certa frequenza (che come vedremo nulla ha a che vedere con la banda passante) l’amplificatore non riesce più a “seguire” le variazioni del segnale, presentando in uscita un segnale con una forma diversa da quello in ingresso.

L’insieme di questi due concetti è sintetizzato in un parametro degli OpAmp che definisce le caratteristiche che deve avere il segnale di ingresso per non ottenere un’uscita distorta: la “slew rate” cioè la massima variazione dell’uscita nell’unità di tempo.

In questo articolo mostreremo con delle simulazioni gli effetti della slew rate su segnali sinusoidali, ricordando che un segnale periodico è composto dalla somma di infinite sinusoidi e che la risposta di un amplificatore ad un segnale può essere calcolato con la sovrapposizione degli effetti delle singole risposte.

Risposte a segnali sinusoidali

In Figura 1 è mostrato il circuito utilizzato nel simulatore LTspice per determinare gli effetti della limitazione della slew rate applicando un ingresso sinusoidale ad un OpAmp OP492 della Analog Devices in configurazione invertente. Fissata la frequenza del segnale di ingresso si esegue una simulazione parametrica con diversi valori dell’ampiezza (0.1 0.5 1 1.3) per poter confrontare le uscite nelle differenti condizioni.

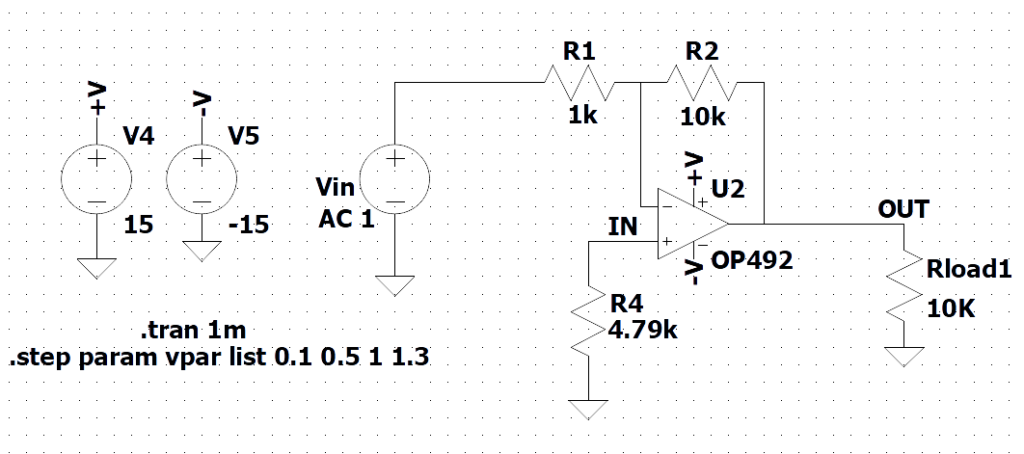
Figura 1: Circuito di test

Perché usare un ingresso sinusoidale ad ampiezza variabile? Cerchiamo prima di capire cosa è la slew rate e come è legata ad ampiezza e frequenza dei segnali in ingresso. Se consideriamo una sinusoidale v(t)=Vsin(ωt) la sua variazione nell’unità di tempo è data dalla derivata: Vωcos(ωt). Il valore massimo della derivata, ovvero della variazione nell’unità di tempo della sinusoide, è pari al prodotto Vω e si misura in V/µs. Conoscendo il guadagno e la massima tensione di uscita si ottiene la massima tensione di ingresso applicabile per la frequenza data. Allo stesso modo, conoscendo la massima ampiezza del segnale in ingresso e l’amplificazione si ottiene la massima frequenza amplificabile senza distorsioni. Questa frequenza prende il nome anche di banda passante a piena potenza e dovrebbe ormai essere chiaro che è un parametro diverso dalla banda passante (legata all’amplificazione o meno dei segnali). In Figura 2 è mostrata la risposta in frequenza del circuito di test, che presenta un guadagno uguale 10 (ovvero 20 dB) fino a circa 100kHz. Ci aspetteremmo di avere sinusoidi in uscita sempre pari a 10 volte quelle in ingresso fino a questa frequenza, se non ci fosse la presenza di una slew rate di 3V/µs per l’OpAmp considerato.

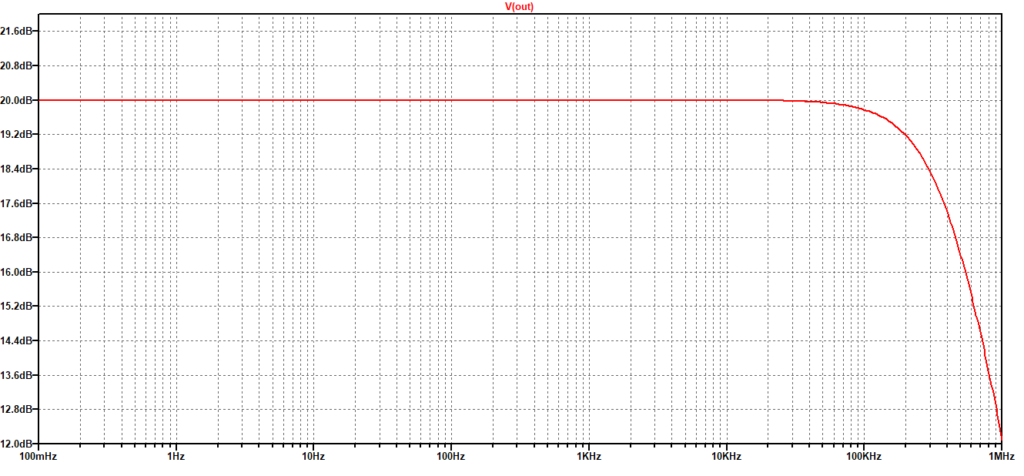
Figura 2: Risposta in frequenza

Nella Figura 3 si vede come la risposta sia lineare fino alla massima tensione di uscita per segnali di frequenza 20kHz. Infatti il prodotto Vω in questo caso vale (13*2*π*20000)/10000000, ovvero circa 1.6 V/µs quindi minore della slew rate.

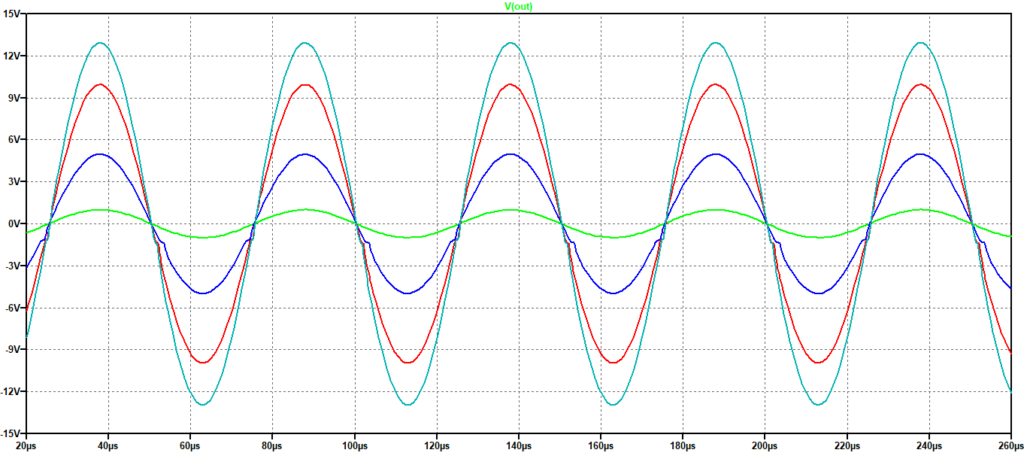
Figura 3: Risposta ad una sinusoide. Frequenza: 20 kHz

Facendo qualche calcolo vediamo che con un ingresso di ampiezza di 1 V (di picco) avremo un’uscita di ampiezza massima 10 V: sostituendo quest’ultimo valore nella formula della slew rate: Vω<3 si determina una frequenza massima di circa 47kHz. Nella Figura 4 vediamo la risposta a sinusoidi di frequenza 50kHz. Si nota per la sinusoide a massima ampiezza una leggera distorsione.

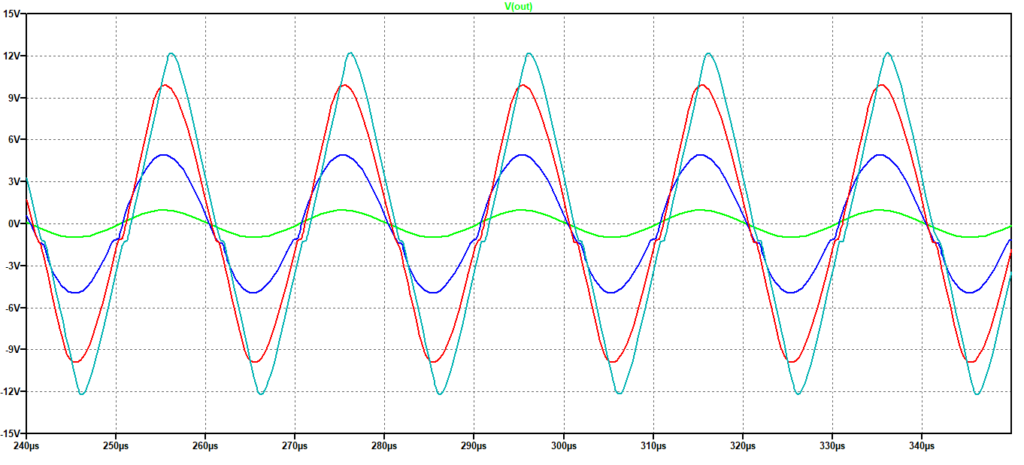
Figura 4: Risposta ad una sinusoide. Frequenza: 50 kHz

Nella successiva Figura 5 invece è possibile apprezzare la distorsione dei segnali con ampiezza 1 e 1.3 V: le uscite somigliano più ad onde triangolari che a sinusoidi!

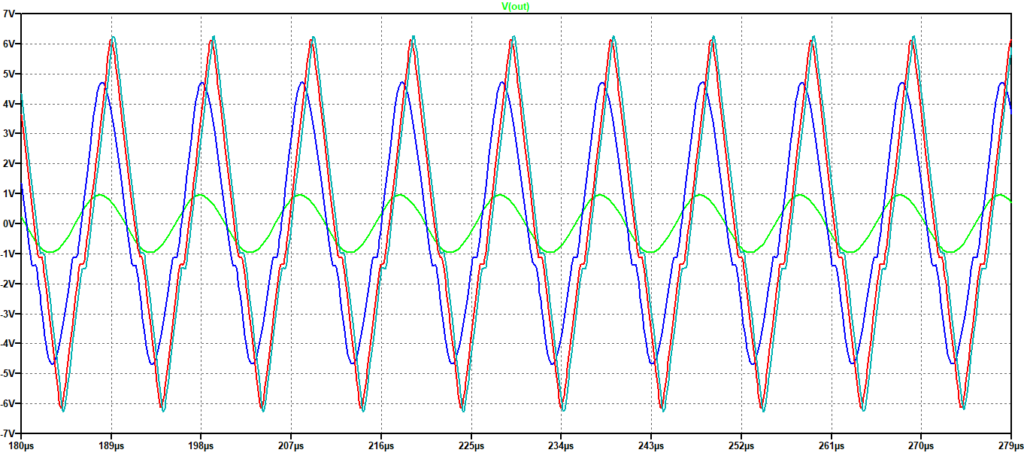
Figura 5: Risposta ad una sinusoide. Frequenza: 100 kHz

Nella Figura 6 si vede come la risposta sia lineare solo per l’ingresso a 0.1 V, con un valore di guadagno in linea con la risposta in frequenza. In questo esempio risulta maggiormente evidente come il concetto di banda passante sia “incompleto” se non si tiene in conto anche l’ampiezza del segnale.

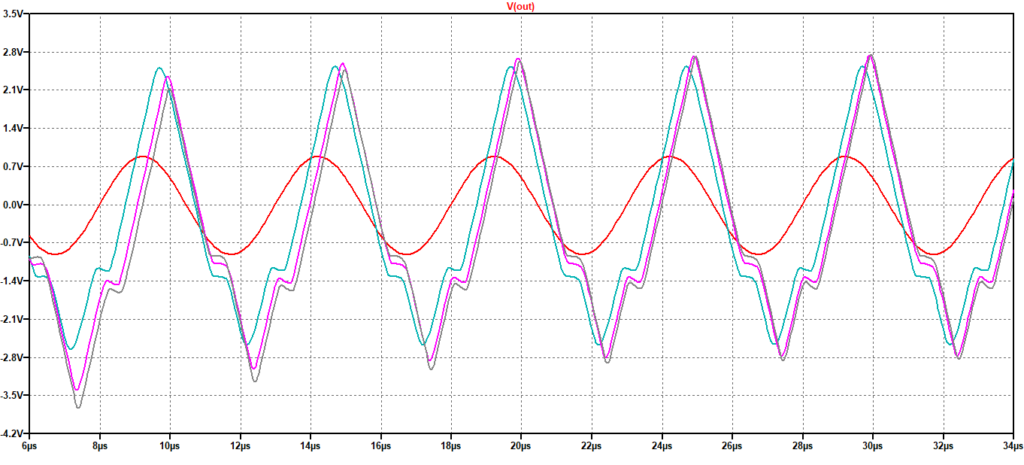
Figura 6: Risposta ad una sinusoide. Frequenza: 200 kHz

Risposta al gradino

Nelle successive figure sono riportate le risposte ad un segnale che varia a gradino in modo da mostrare in un altro modo gli effetti del limite alla velocità di variazione del segnale di uscita per ampie variazioni. Il segnale in ingresso varia da 0 a 1.2 V con tempi diversi, come riportato nelle didascalie, con l’uscita che risulta pari all’ingresso amplificato solo quando la velocità della variazione (il tempo per passare da 0 a 1.2 V) è inferiore alla slew rate. Negli altri casi, oltre una evidente distorsione, l’uscita raggiunge il massimo in tempi successivi all’ingresso.

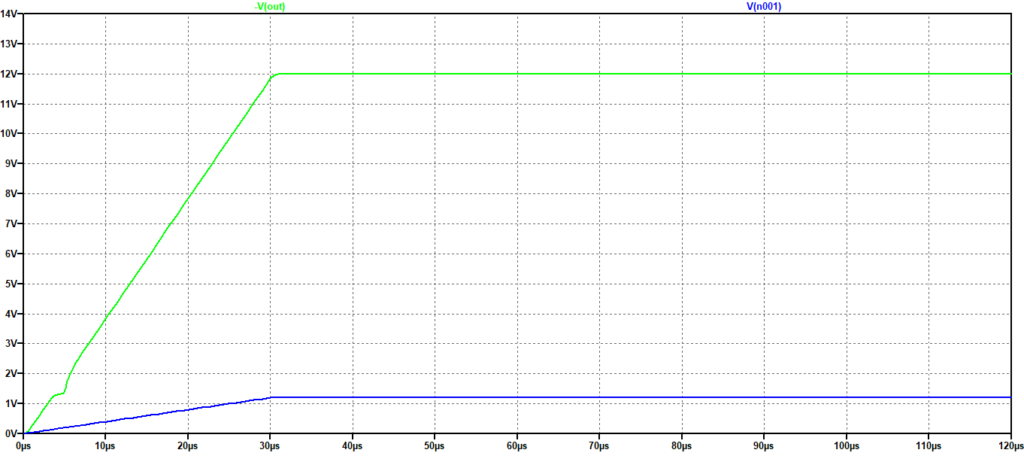
Figura 7: Risposta ad un gradino. Temnpo di salita: 30 us

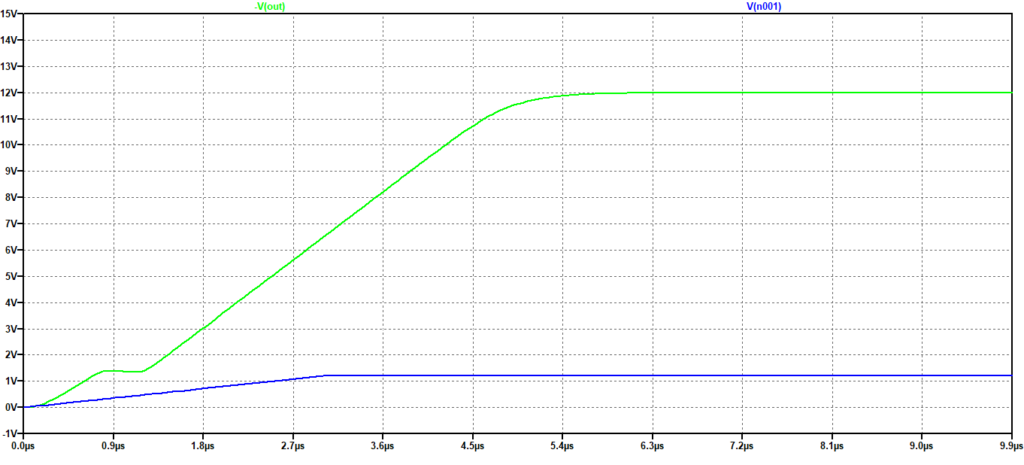
Figura 8: Risposta ad un gradino. Tempo di salita: 3 us

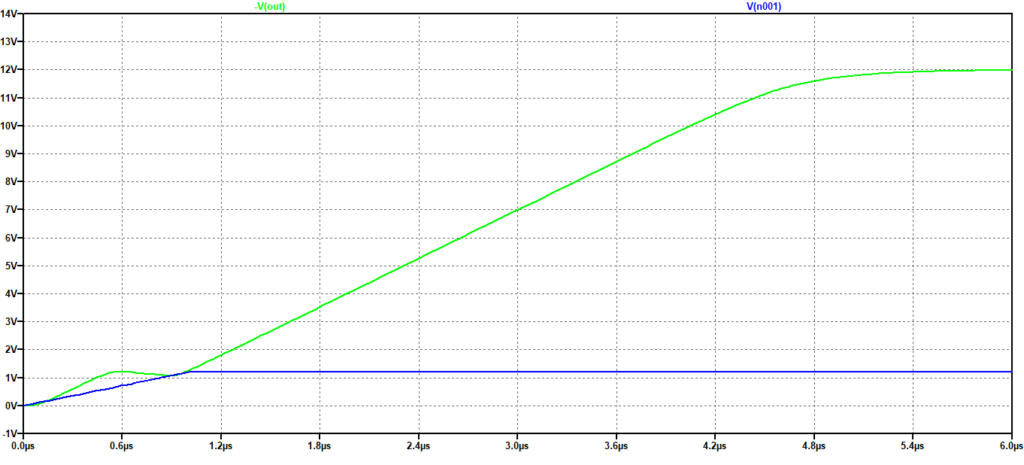
Figura 9: Risposta ad un gradino. Tempo di salita: 1 us

Conclusioni

Un amplificatore non può rispondere linearmente, cioè senza distorsione, a segnali di ingresso che abbiano armoniche con pendenza superiore alla slew rate. Questo parametro è pari al prodotto dell’ampiezza massima del segnale di uscita per la sua banda (ovvero della massima frequenza presente nel segnale) che prende, quindi, anche il nome di banda passante a piena potenza. Considerando le risposte a segnali a gradino, o onda quadra, si può apprezzare l’effetto della slew rate come dovuto al ritardo di propagazione del segnale fra l’ingresso e l’uscita.