Parte 1: relazione fra guadagno e banda passante
Gli Amplificatori Operazionali servono per amplificare ed elaborare segnali che variano nel tempo e non solo grandezze continue. Idealmente il guadagno dovrebbe essere lo stesso indipendentemente dalla frequenza del segnale di ingresso ma, come qualunque sistema dinamico, l’amplificazione dipende dalla frequenza del segnale applicato.
Risposta in frequenza a ciclo aperto
In Figura 1 è mostrata la risposta in frequenza a ciclo aperto dell’OpAmp OP492 della Analog Devices. Come quasi tutti gli OpAmp moderni si comporta come un sistema del primo ordine, con un guadagno costante in bassa frequenza e poi una diminuzione di 20 dB/dec, corrispondente ad un andamento proporzionale ad 1/ω. Questa caratteristica è ottenuta grazie ad un condensatore integrato all’interno del circuito con un valore tale da rendere trascurabili le capacità parassite dei vari transistors; in questo modo si garantisce la stabilità del circuito per un ampio intervallo di frequenze proprio come se fosse un sistema con un singolo polo dominante.
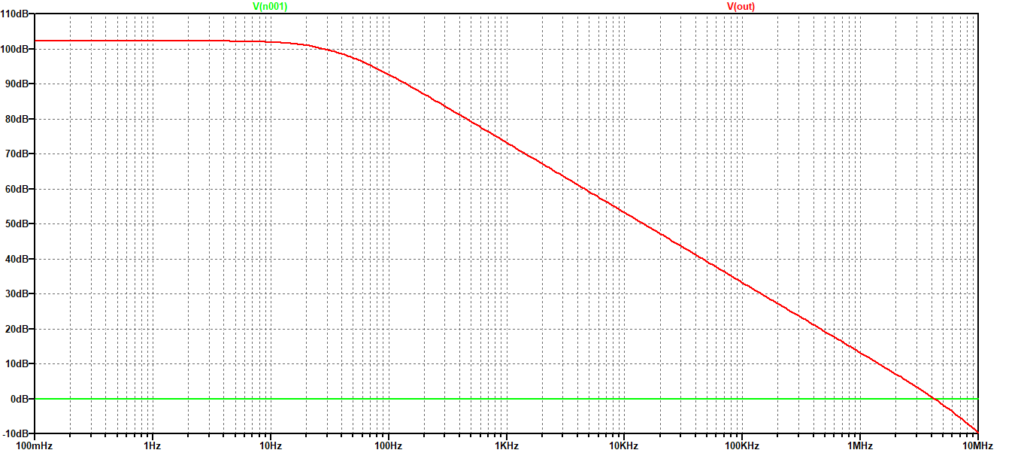
Figura 1: Risposta in frequenza a ciclo aperto
Come si concilia questa relativamente ridotta banda passante con applicazioni che richiedono una banda molto più estesa? Sfruttando le proprietà della retroazione! Ricordiamo che un OpAmp ha senso se inserito in un circuito e soprattutto che (entro certi limiti, come visto negli articoli precedenti) la caratteristica di trasferimento Vout/Vin dipende dal circuito esterno. Come esempio utilizziamo un circuito amplificatore invertente, mostrato in Figura 2.
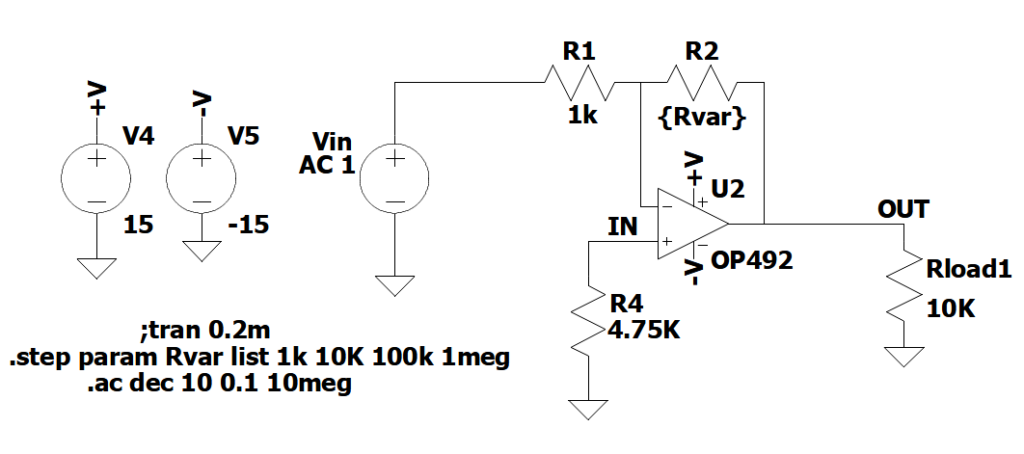
Figura 2: Circuito di test – Amplificatore in configurazione invertente
In questo caso, con le ipotesi di idealità dell’OpAmp (che possiamo ritenere soddisfatte per la scelta dei resistori) si ha:
i(R1)=Vin/R1
Vout =i(R2) * R2 = -i(R1) * R2 = -Vin*R2/R1
Risposta in frequenza a ciclo chiuso
Analizziamo ora il circuito dal punto di vista della retroazione e scriviamo la formula del guadagno a ciclo chiuso:
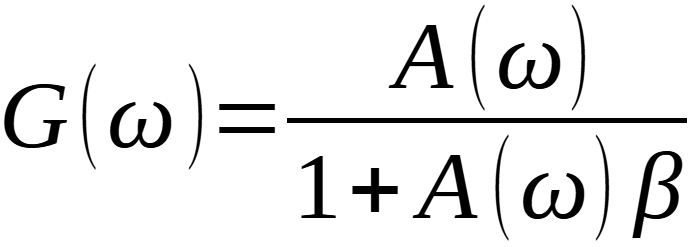
Fintanto che A(ω)β>>1 si può approssimare G(ω)=1/β, come in continua, mentre per A(ω)β<<1 si trascura questo termine ed il guadagno a ciclo chiuso è approssimato dal valore a ciclo aperto. In quest’ultimo caso si ha che svanisce l’effetto della retroazione (ed ancora una volta è evidente l’effetto dell’elevato guadagno a ciclo aperto sul funzionamento dei circuiti con OpAmp). Nell’ipotesi che risposta a ciclo aperto sia del primo ordine, come mostrato in Figura 1, si ha che anche la risposta a ciclo chiuso lo è e si può ottenere un interessante legame fra la banda passante (a -3 dB) ed il guadagno a ciclo chiuso. Come detto, per frequenze “elevate”, oltre la banda passante a ciclo aperto, si può approssimare A(ω)=A/ω (con A guadagno a ciclo aperto in continua), di conseguenza:
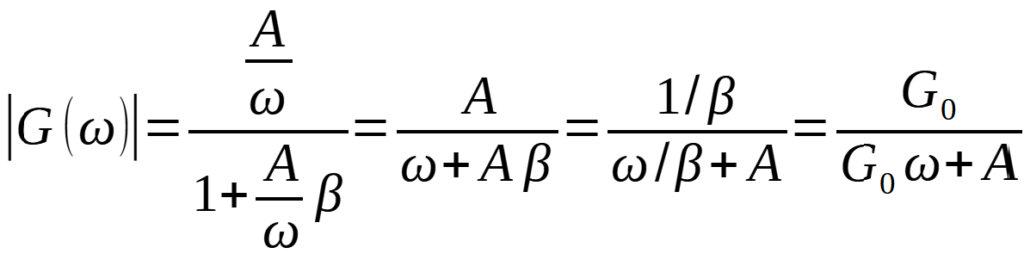
che è tipica di un sistema con un polo dominante. Quindi per ω<<Aβ si ha un guadagno a ciclo chiuso pari a G=1/β, come visto in precedenza, mentre per:
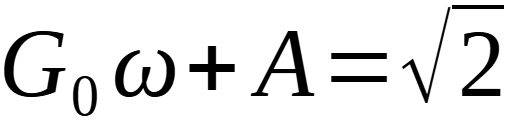
si ha:
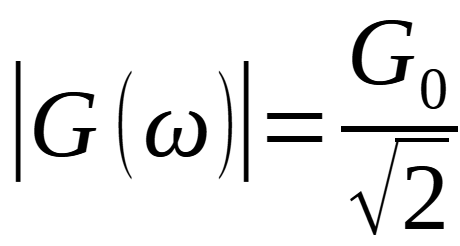
che corrisponde ad una attenuazione di 3 dB.
Perché è considerata importante questa frequenza
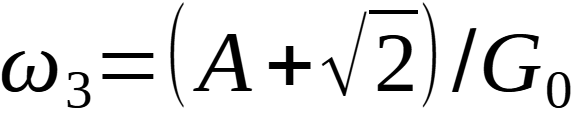
che viene anche considerata “banda passante”? Il quadrato del modulo di G corrisponde al rapporto fra la potenza in uscita e quella in ingresso ed a 3 dB si ha un’attenuazione pari alla metà. Questo valore è legato alla capacità dell’orecchio umano di distinguere i suoni ed al fatto che i primi amplificatori sono stati pensati per applicazioni audio. La conseguenza più importante per i progettisti di circuiti è, invece, che il prodotto del guadagno per la banda passante è costante ed è caratteristico di ogni OpAmp, indicato tipicamente sui data sheet come GBP (Gain Bandwidth Product).
Possiamo verificarlo con una simulazione in LTSpice, usando il circuito di Figura 2, facendo variare il guadagno cambiando il valore della resistenza R2. Per effettuare una simulazione parametrica si esprime il valore del parametro, ovvero della resistenza in questo caso, con un nome arbitrario fra parentesi graffe. Nell’esempio {Rvar}. Si aggiunge il comando .step per la simulazione, indicando il parametro ed i rispettivi valori:
.step param Rvar list 1k 10k 100 k 1meg
In questo modo si ottengono quattro simulazioni,per guadagni pari a 1, 10, 100, 100. Le relative risposte in frequenza sono mostrate nella Figura 3.
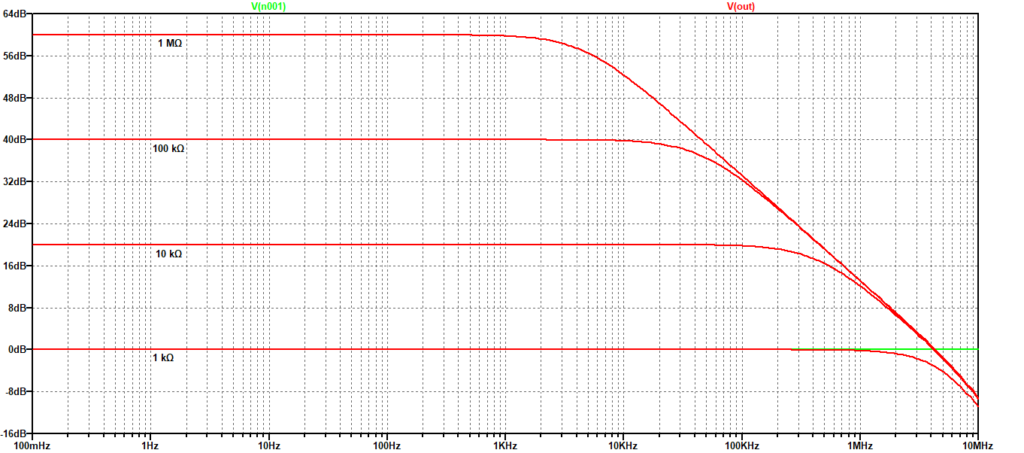
Figura 3: Risposta in frequenza a ciclo chiuso al variare del guadagno
Come si può vedere il prodotto Guadagno x Banda è circa 4, in accordo al valore riportato sul data sheet dell’OP492. Simulando un ingresso sinusoidale possiamo indagare come varia la risposta al variare del guadagno per diverse frequenze. Nelle successive Figura 4 e Figura 5 sono riportate le risposte ad un ingresso sinusoidale di ampiezza 10 mV e frequenza 10 Hz e 10 Khz, rispettivamente. Dal confronto si vede come la risposta di guadagno più elevato diminuisca all’aumentare della frequenza, mentre le altre restino all’incirca uguali, in accordo con i valori desumibili dal grafico di Figura 3. Questi risultati si possono leggere anche in un altro modo: se il guadagno è basso, per ottenere valori elevati in uscita dobbiamo avere in ingresso segnali di ampiezza già elevata, viceversa non possiamo sperare di avere in uscita segnali di ampiezza significativa.
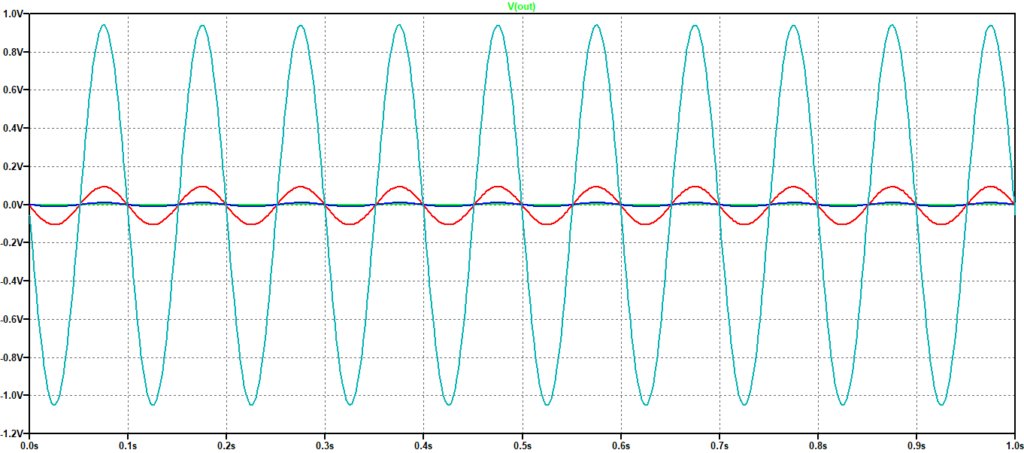
Figura 4: Risposta ad una sinusoide di ampiezza 10mV e frequenza 10Hz
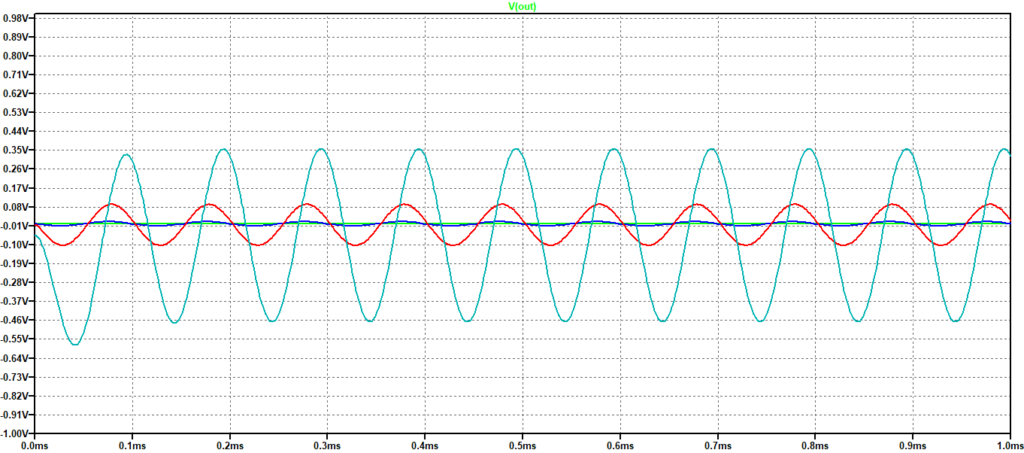
Figura 5: Risposta ad una sinusoide di ampiezza 10mV e frequenza 10kHz
Conclusioni
La possibilità di amplificare segnali variabili nel tempo, e non solo continui, si scontra con la banda finita degli OpAmp. Questa apparente limitazione può essere superata sfruttando le proprietà della retroazione scegliendo un opportuno valore di guadagno a ciclo chiuso. Abbiamo visto, infatti, che una caratteristica degli Amplificatori Operazionali è il prodotto Guadagno per Banda, per cui si può sfruttare una banda maggiore a costo di un guadagno inferiore. Come sempre resta a cura del progettista la scelta del miglior compromesso.
















