La simulazione dell’analisi AC è una tecnica utilizzata per analizzare il comportamento di un circuito elettrico nel dominio della frequenza. Essa è utile per studiare la risposta in frequenza di un circuito, ovvero come le sue caratteristiche cambiano al variare della frequenza del segnale di ingresso. L’analisi AC può essere utilizzata per studiare una grande varietà di circuiti, inclusi circuiti lineari e non lineari, circuiti attivi e passivi. Inoltre essa è particolarmente utile nella progettazione di circuiti oscillatori, amplificatori e filtri.
La reattanza capacitiva di un condensatore
La reattanza capacitiva è una proprietà dei condensatori che si manifesta quando questi sono attraversati da una corrente alternata ed è rappresentata dalla sigla Xc e si misura in ohm, proprio come un resistore. La formula per calcolare la reattanza capacitiva è la seguente:
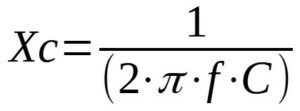
dove:
Xc = reattanza capacitiva, misurata in ohm;
C = capacità del condensatore in farad;
f = frequenza del segnale.
La reattanza capacitiva è inversamente proporzionale alla frequenza del segnale alternata. All’aumentare della frequenza, la reattanza capacitiva diminuisce. La reattanza capacitiva è anche inversamente proporzionale alla capacità del condensatore. Ciò significa che, all’aumentare della capacità del condensatore, la reattanza capacitiva diminuisce. La reattanza capacitiva è una proprietà molto importante dei condensatori ed è utilizzata in una varietà di applicazioni, come la progettazione dei filtri e dei circuiti di sintonia. Si inizi a esaminare lo schema elettrico di figura 1, che contiene un collegamento in serie tra un resistore e un condensatore. Esso è composto dai seguenti componenti:
-
- V1: il generatore ideale sinusoidale, dalla tensione di 12 Vpp e dalla frequenza di 50 Hz;
- R1: il resistore ideale di 50 ohm;
- C1: il condensatore ideale di 100 microFarad;
- N01 e N02: nodi per la misura delle tensioni.
Lo schema contiene alcune direttive SPICE per il corretto funzionamento:
-
- “.tran 1”:
- “.plot v(N01),v(n02)”:
La direttiva “.tran” specifica il tipo di analisi transitoria per la durata di 1 secondo, ovvero si analizza il comportamento del circuito nel tempo. La direttiva .plot, invece, specifica quali variabili si desidera mostrare nel grafico, nell’esempio le tensioni presenti ai nodi N01 e n02.
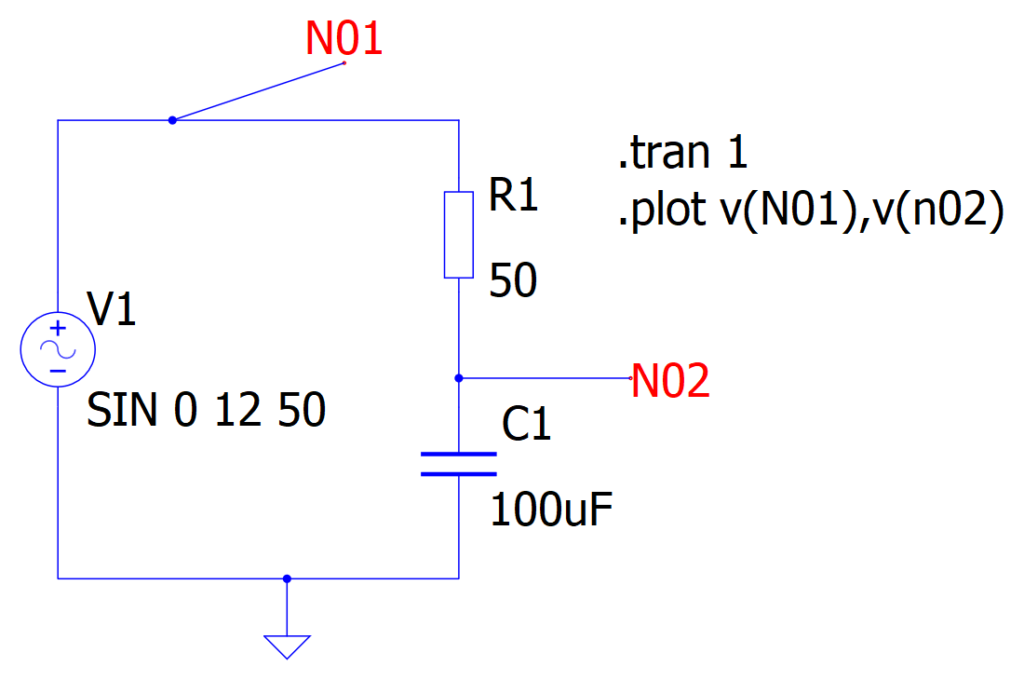
Figura 1 – Il circuito contiene un collegamento in serie tra un resistore e un condensatore.
Come si vede nel grafico di figura 2, alla frequenza del generatore dello schema elettrico e alla capacità del condensatore C1, quest’ultimo si comporta quasi come un resistore, formando un partitore assieme a R1. Con la formula prima esaminata, la reattanza capacitiva è di 31.831 ohm e la tensione prelevata al nodo centrale del partitore è, ovviamente, più bassa rispetto a quella del generatore sinusoidale.
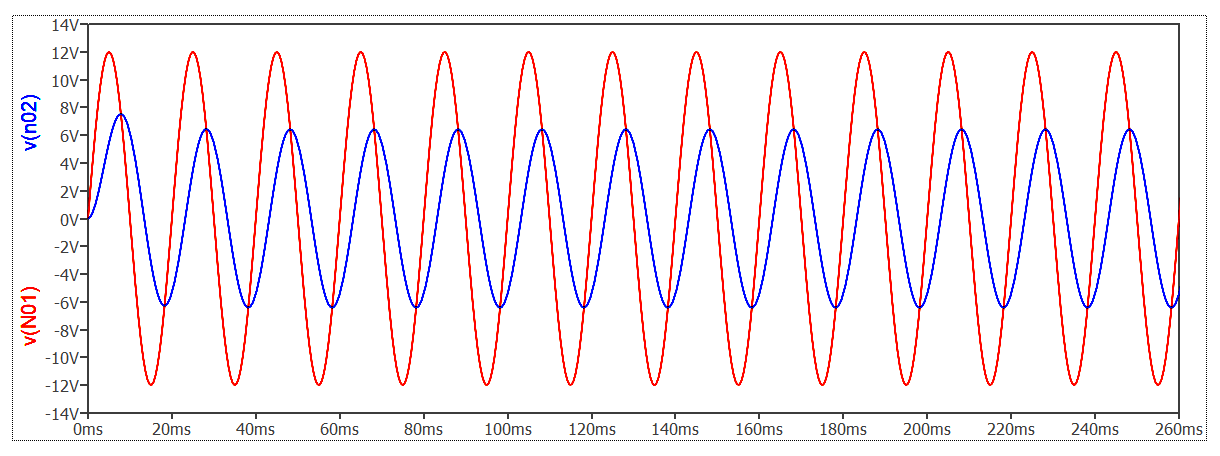
Figura 2 – La tensione sinusoidale prelevata al nodo centrale del partitore.
Teoricamente, il condensatore di 100 microFarad dello schema elettrico, alla frequenza di 50 Hz corrisponde a un resistore di 31.831 ohm, per cui uno schema quasi equivalente potrebbe essere quello proposto in figura 3. Ovviamente i condensatori non sono componenti lineari, pertanto causano un certo sfasamento o ritardo nel segnale, rispetto ai resistori che, al contrario, sono componenti dal funzionamento perfettamente lineare.
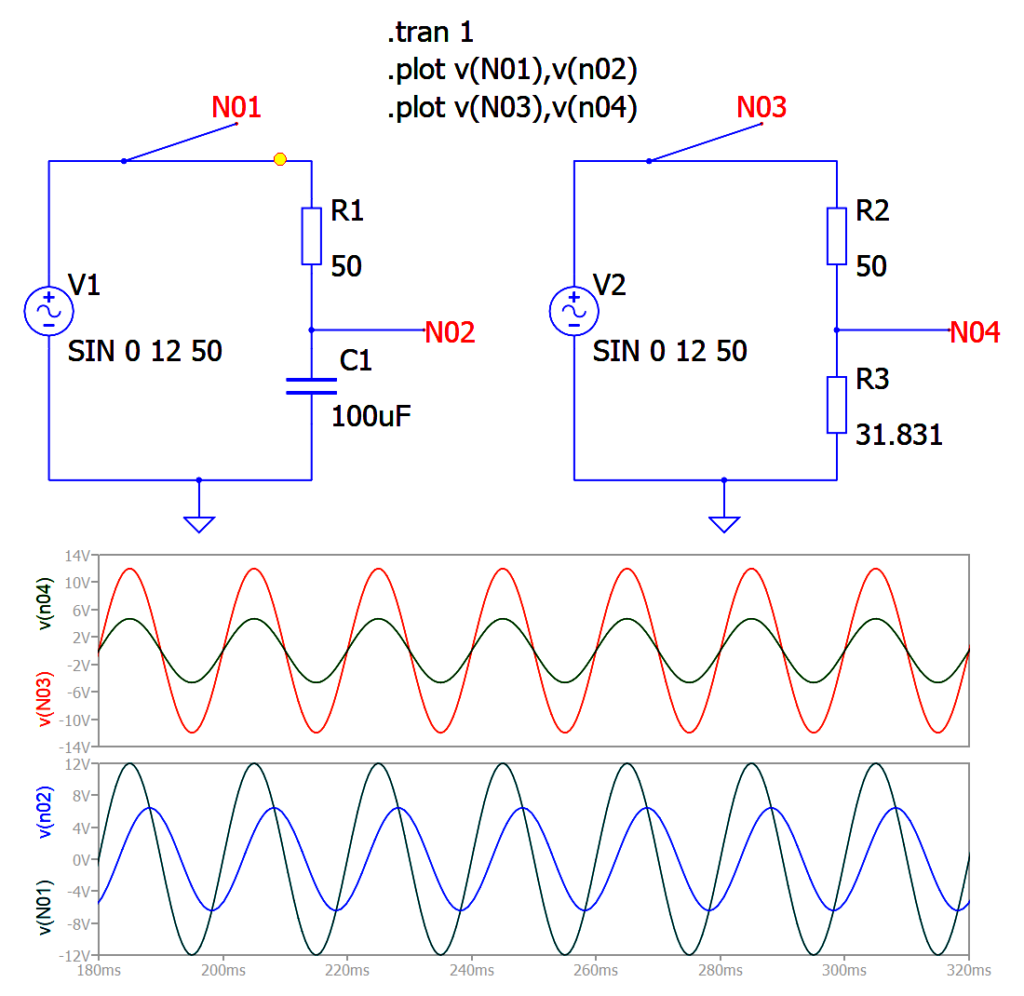
Figura 3 – Un condensatore in regime alternato è quasi simile a un resistore.
La direttiva “.AC”
Come detto prima, questa direttiva consente di calcolare la risposta del circuito nel dominio della frequenza. Per attivare questa funzionalità occorre eseguire due modifiche al circuito precedente:
-
- “.AC” è la direttiva SPICE vera e propria e calcola le tensioni dei nodi complessi AC in funzione della frequenza;
- “lin” esegue una analisi lineare tra la frequenza minima e la frequenza massima;
- 100 è il numero di punti considerati nell’analisi. Per le tipologie “oct” e “dec” tale parametro indica il numero di passi, rispettivamente, per ogni ottava oppure per ogni decade;
- 5 è la frequenza minima da cui la simulazione inizia;
- 200 è la frequenza massima a cui la simulazione termina.
Dopo aver avviato la simulazione, sullo schermo viene visualizzata l’analisi in frequenza relativamente ai due nodi N01 (tensione del generatore sinusoidale) e N02 (tensione sul partitore), come è ben evidenziato in figura 4. Il grafico è molto interessante è mostra le seguenti curve:
-
- grafico rosso con cerchio pieno (scala a sinistra in dB): tensione fissa del generatore al nodo N01 (21.583625 dB);
- grafico rosso con cerchio vuoto (scala a destra in gradi): fase fissa della tensione del generatore al nodo N02 (0°);
- grafico blu con cerchio pieno (scala a sinistra in dB): tensione variabile del generatore al nodo N02 all’aumentare della frequenza;
- grafico blu con cerchio vuoto (scala a destra in gradi): fase variabile della tensione del generatore al nodo N02.
In QSPICE i valori della tensione, come si vede, possono essere espressi in dB oppure i volt ma in scala logaritmica. Esiste una precisa corrispondenza tra i volt e i dB (più precisamente dBV) e viceversa. Le due formule di conversione sono le seguenti:
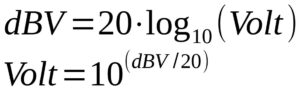
La seguente tabella mostra, invece, alcune tensioni elettriche convertite nei rispettivi valori dBV. Questa conversione è utile per confrontare i valori di tensione tra diverse misurazioni.
| Volt | dBV |
| 1 uV | -120 |
| 1 mV | -60 |
| 10 mV | -40 |
| 100 mV | -20 |
| 1 V | 0 |
| 2 V | 6.0206 |
| 3 V | 9.5424 |
| 4 V | 12.0412 |
| 5 V | 13.9794 |
| 6 V | 15.5630 |
| 7 V | 16.9019 |
| 8 V | 18.0618 |
| 9 V | 19.0848 |
| 10 V | 20 |
| 11 V | 20.8278 |
| 12 V | 21.5836 |
| 100 V | 40 |
| 1000 V | 60 |
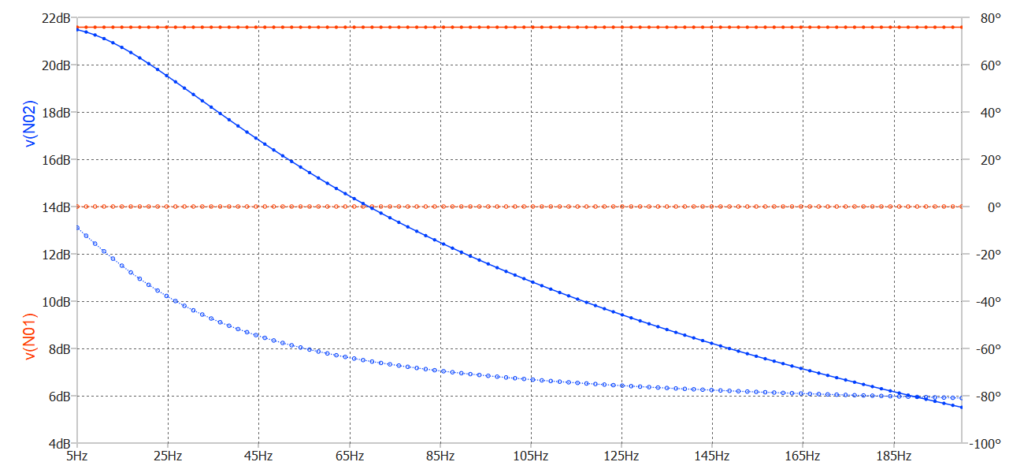
Figura 4 – L’analisi AC dello schema in esame.
La frequenza può essere visualizzata in fattori di 8, di 10 oppure in modo lineare o, ancora, specificando una lista di valori fissi. Di seguito sono riportate le relative sintassi di utilizzo:
.ac oct N FREQ1 FREQ2
.ac dec N FREQ1 FREQ2
.ac [lin] N FREQ1 FREQ2
.ac list FREQ1 FREQ2 FREQ3 …
Se non viene specificato nessun parametro “oct”, “lin” o “list”, il software eseguirà una simulazione lineare.
Simulazione di un filtro passa basso
La direttiva “.AC” è molto utile per la simulazione e l’osservazione della risposta in frequenza di un filtro passa basso, cioè un circuito molto importante per fare passare solo le basse frequenze ed eliminare le armoniche superiori. Questo tipo di filtro consente solo a segnali a bassa frequenza da 0 Hz alla sua frequenza di taglio (fc) di passare, bloccando quelli a frequenza più alta. In figura 5 si può osservare un tipico filtro passa basso, che poi è equivalente allo schema del precedente paragrafo. Come si evince dallo schema elettrico, è possibile creare dei semplici filtri passivi di primo ordine collegando in serie un resistore a un condensatore e prelevando l’uscita dalla giunzione di questi due componenti. A seconda del tipo di collegamento tra il resistore e il condensatore, si determina il filtro passa-basso oppure il filtro passa-alto.
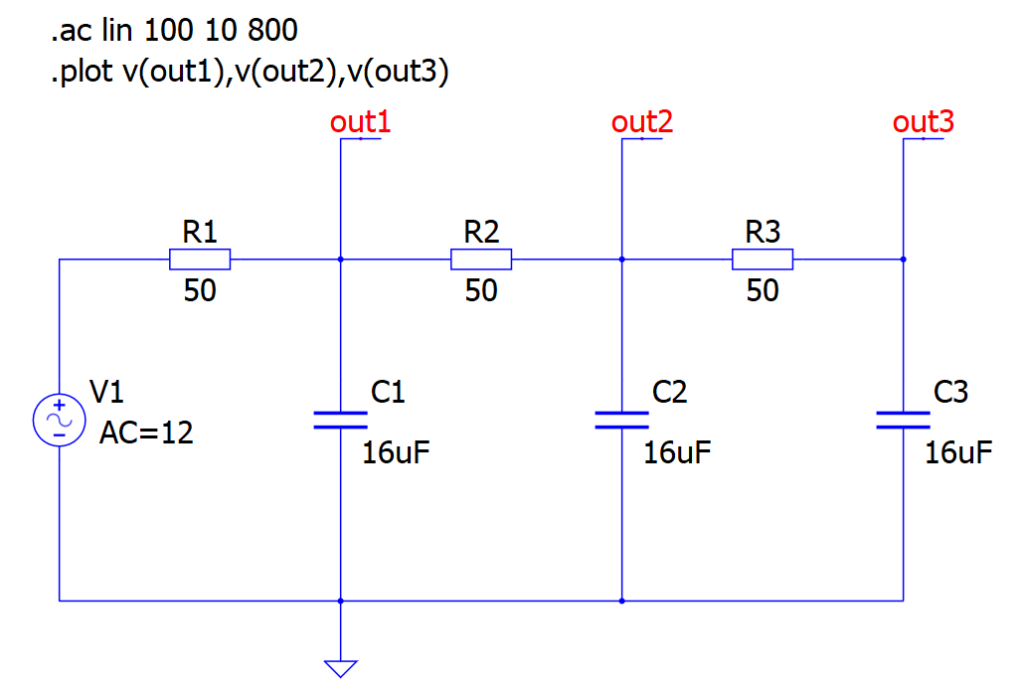
Figura 5 – Un semplice filtro passa basso composto da tre celle collegate in cascata.
In questo caso, per semplicità, il filtro è composto da due tipi principali di componenti, ossia da resistori e da condensatori. Questi componenti possono essere collegati in serie o in parallelo, a seconda delle necessità dell’applicazione. Per il calcolo dei componenti dei filtri esiste una apposita letteratura e vi sono anche molti tools, software e calcolatori che aiutano l’utente nella progettazione. Le formule principali per il calcolo dei componenti e della frequenza di taglio sono le seguenti:
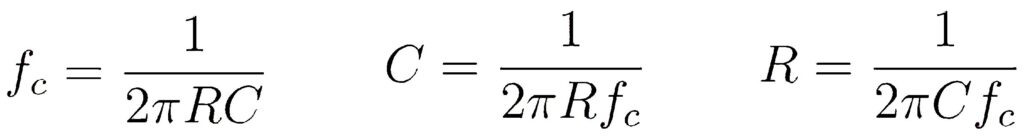
Il filtro dell’esempio contiene tre moduli in cascata ed è caratterizzato dai seguenti elementi:
-
- V1: segnale sinusoidale;
- R1, R2, R3: resistore da 50 ohm;
- C1, C2, C3: condensatore da 16 uF.
Con questi componenti la frequenza di taglio è di circa 200 Hz. Le direttive SPICE utilizzate nello schema elettrico sono le seguenti:
.ac lin 100 10 800
.plot v(out1),v(out2),v(out3)
Lo schema elettrico prevede tre diverse uscite del segnale, da dove si può prelevare il segnale filtrato (out1, out2 e out3). Out3 ha un tasso di filtraggio maggiore di out2 che, a sua volta, ha un tasso di filtraggio maggiore di out1. La figura 6 mostra le curve di risposta del filtro alle varie frequenze, in scala logaritmica. Aumentando la complessità del circuito, o il numero delle celle che lo compongono, il tasso di filtraggio sarà anch’esso più elevato. Per elevati ordini di filtro, non è più conveniente utilizzare solo componenti passivi ma è consigliabile usare amplificatori operazionali e componenti attivi.
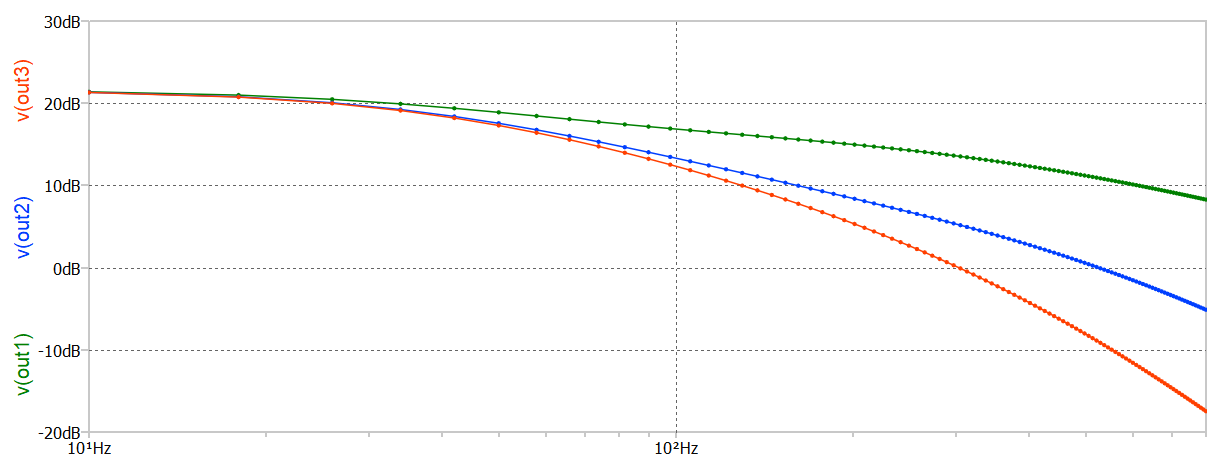
Figura 6 – Le risposte in frequenza del filtro passa basso, alle tre uscite.
Filtro passa banda passivo per la ricezione dei satelliti polari
L’ultimo esempio dell’articolo illustra la realizzazione e la simulazione di un filtro passa banda passivo RLC. Come è possibile osservare in figura 7, esso è composto esclusivamente da resistori, induttanze e condensatori. Il filtro passa banda RLC seleziona e lascia passare solo un intervallo di frequenze, attenuando quelle inferiori e quelle superiori rispetto alla frequenza di taglio. Nell’esempio proposto, il filtro può essere impiegato per la ricezione del segnale radio dei satelliti polari, operanti alla frequenza di 137 Mhz. Il filtro utilizza induttori e condensatori dal valore estremamente basso, per cui la sua realizzazione dovrebbe seguire criteri di precisione e montaggio SMD.
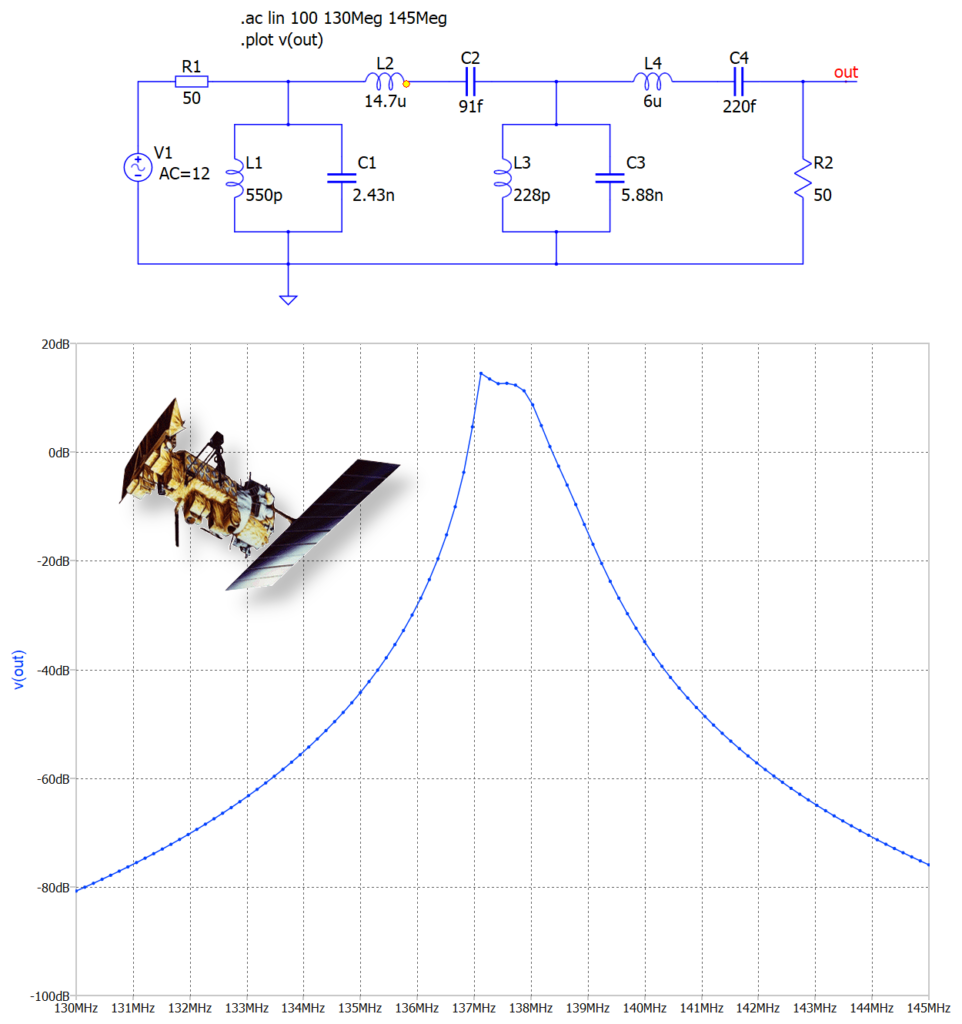
Figura 7 – Lo schema elettrico del filtro passa banda per la ricezione dei satelliti polari.
Le direttive SPICE utilizzate nello schema elettrico sono le seguenti:
.ac lin 100 130Meg 145Meg
.plot v(out)
Conclusioni
Come si può ben comprendere, l’analisi “.AC” di QSPICE è uno strumento molto potente e ha lo scopo di analizzare la risposta in frequenza dei circuiti elettronici, in regime alternato. Tale analisi consente di valutare il comportamento degli schemi elettronici in diverse situazioni di frequenza e di ottimizzare le prestazioni del circuito. Essa è particolarmente utile specialmente per la progettazione dei filtri e degli amplificatori.
Autore: Giovanni Di Maria















