Gli Amplificatori Operazionali sono circuiti integrati noti per la capacità di realizzare le più disparate funzionalità utilizzando pochi componenti esterni: con una opportuna rete di retroazione si può ottenere un amplificatore dal guadagno desiderato o un circuito dinamico in grado di effettuare operazioni matematiche sui segnali in ingresso, come ad esempio l’integrale.
In questo articolo mostreremo come determinare la velocità di variazione di un segnale mediante un circuito che fornisce in uscita un segnale proporzionale alla sua derivata e poi come effettuare la somma fra due segnali.
Mediante simulazione con LTspice saranno verificati i risultati teorici proposti.
Il derivatore ideale
Analizziamo il circuito mostrato in : con le approssimazioni dell’OpAmp ideale, la corrente erogata dal generatore scorre tutta nel condensatore C e nella resistenza R. Per il cortocircuito virtuale fra gli ingressi (+) e (-) la tensioni ai capi della capacità è pari a Vin. Di conseguenza:
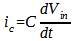
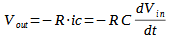
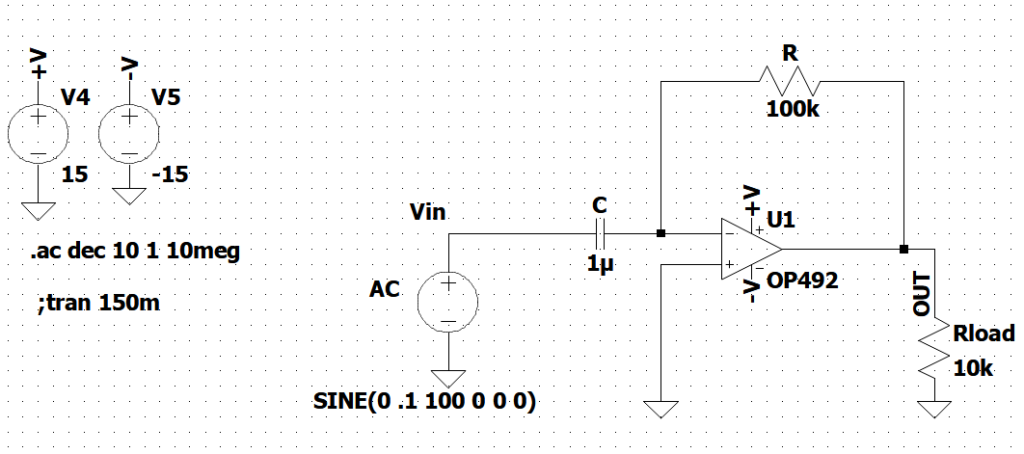
PurtroFigura 1: Derivatore ideale
ppo un tale circuito non può funzionare nella realtà perché il guadagno aumenta all’aumentare della frequenza del segnale. Siccome in natura il rumore è sempre presente a tutte le frequenze si avrebbe in pratica una amplificazione del rumore in alta frequenza e questo non sarebbe accettabile.
Se vediamo lo spettro della risposta in frequenza di questo circuito, mostrata in notiamo che la risposta aumenta proporzionalmente alla frequenza, come previsto per il derivatore, fino ad un valore in cui diventa predominante la dinamica del circuito interno dell’OpAmp che non si può più considerare ideale.
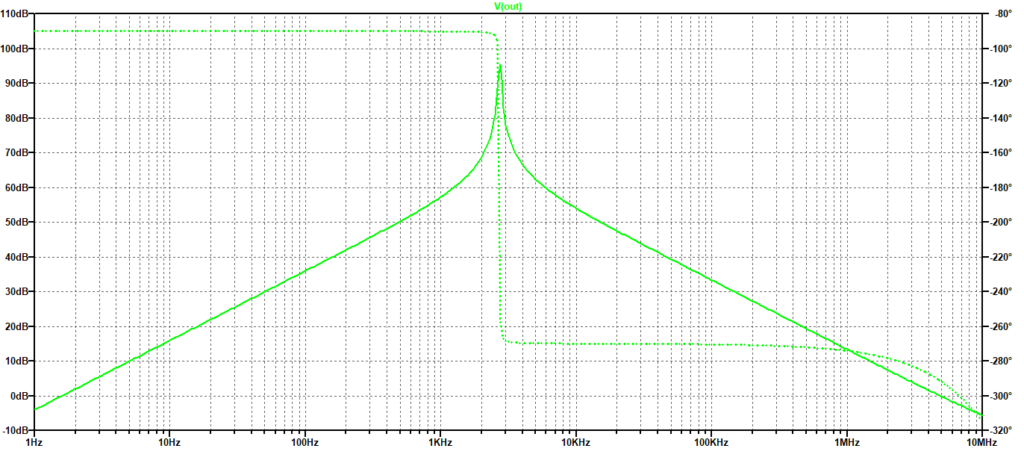 Figura 2: Risposta armonica di un derivatore con OpAmp
Figura 2: Risposta armonica di un derivatore con OpAmp
La presenza di capacità interno all’OpAmp determina addirittura una risonanza che influenza l’uscita in modo deleterio con oscillazioni non desiderate, come mostrato nella successiva.
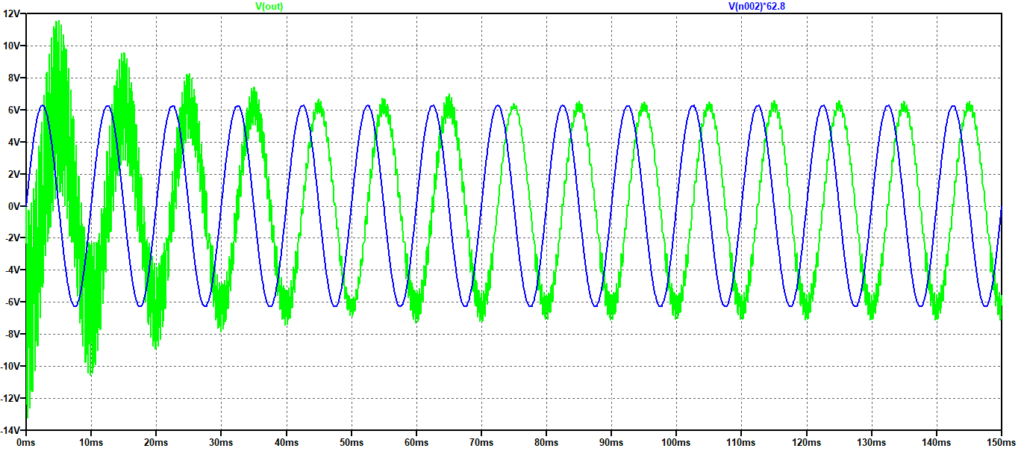 Figura 3: Risposta ad una sinusoide con frequenza 100 Hz
Figura 3: Risposta ad una sinusoide con frequenza 100 HzIl derivatore “pratico”
Un modo di ovviare a questo fenomeno è l’utilizzo di un circuito “passa-alto” che, fissando un limite superiore al guadagno, consente di non amplificare il rumore in alta frequenza, ma soprattutto elimina il comportamento risonante.
Il circuito corrispondente si ottiene inserendo una resistenza in serie al condensatore, come mostrato nella successiva Figura 4.
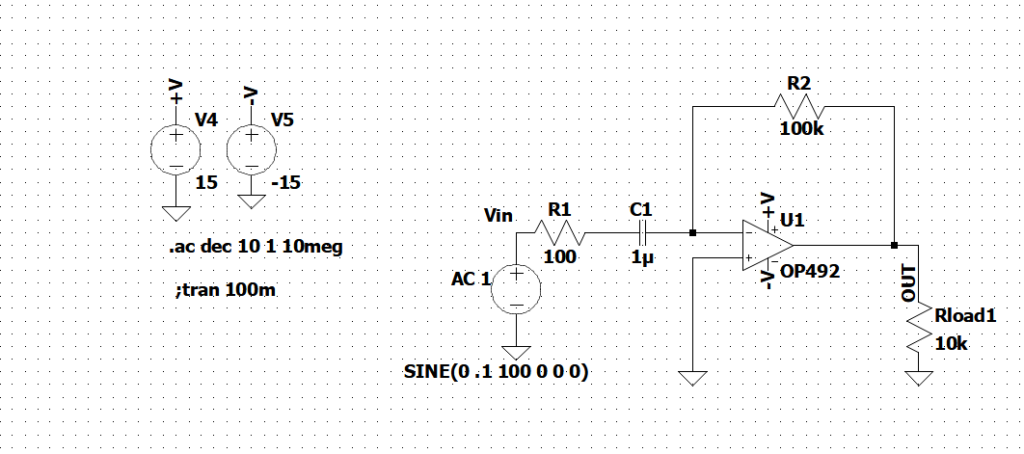 Figura 4: Derivatore “passa-alto”
Figura 4: Derivatore “passa-alto”
Senza dilungarci nei calcoli possiamo verificare di aver migliorato la risposta in frequenza mediante una analisi con LTSpice il cui risultato è mostrato nella successiva Figura 5.
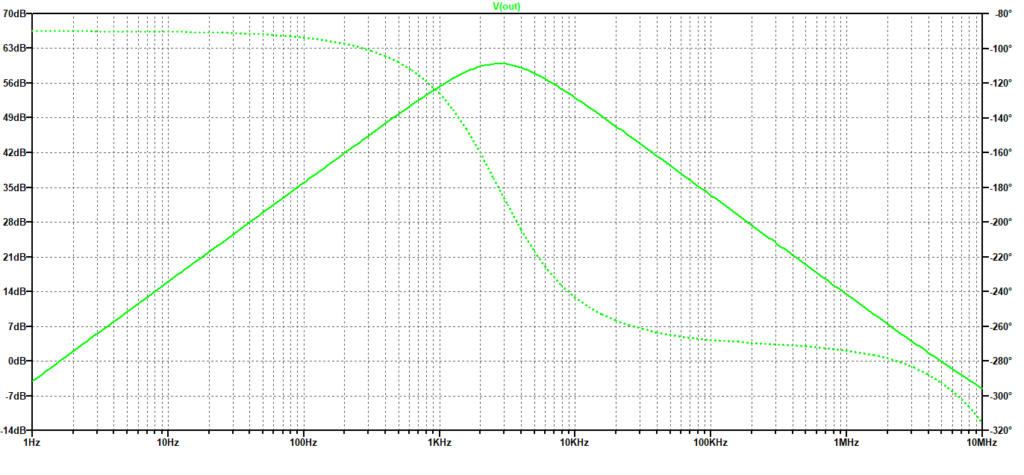
Figura 5: Risposta armonica del derivatore “passa-alto”
Lo spettro ottenuto è quello di un filtro passa-alto seguito da un passa-basso (dovuto alla dinamica interna dell’OpAmp) che può approssimare un derivatore fino a circa 200 Hz (oltre la fase inizia a diminuire ed è inferiore a -90°). Ovviamente i valori delle resistenze e della capacità vanno scelti in funzione della banda e del guadagno desiderato.
Alcune simulazioni ci consentono di valutare la bontà del nostro circuito. In Figura 6 vediamo la risposta ad una sinusoide di frequenza 100 Hz per apprezzare le differenze con il caso precedente, in Figura 7 vediamo come l’uscita sia effettivamente la derivata di un’onda triangolare ed infine si riportano la simulazioni dell’effetto del rumore sull’uscita.
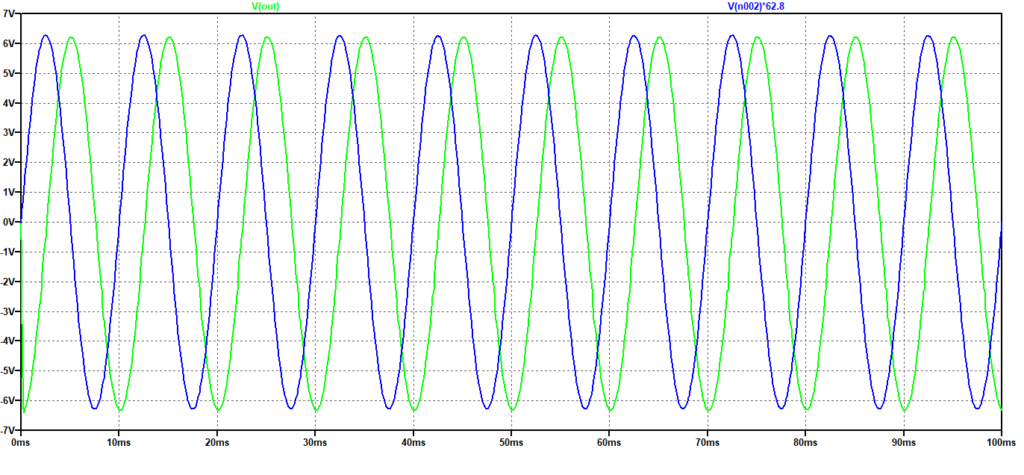 Figura 6: Risposta del derivatore passa-alto ad una sinusoide di frequenza 100 Hz
Figura 6: Risposta del derivatore passa-alto ad una sinusoide di frequenza 100 Hz
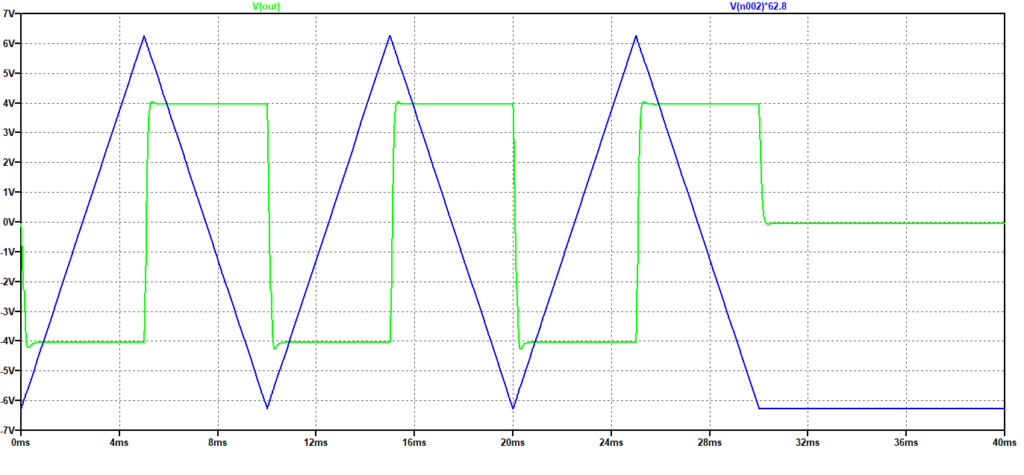 Figura 7: Risposta del derivatore passa-alto ad un’onda triangolare di frequenza 100 Hz
Figura 7: Risposta del derivatore passa-alto ad un’onda triangolare di frequenza 100 Hz
Si noti come l’uscita sia un’onda quadra e diventi nulla quando il segnale diventa costante, come previsto per un segnale proporzionale alla derivata del segnale in ingresso.
Nelle successive Figura 8 e Figura 9 sono riportate rispettivamente le risposte del derivatore “passa-alto” e quella del derivatore “Ideale” visto in precedenza. In blu è visibile il segnale rumoroso in ingresso ed in rosso il solo rumore. Entrambi i segnali sono moltiplicati per 100 per migliorare la visibilità del grafico.
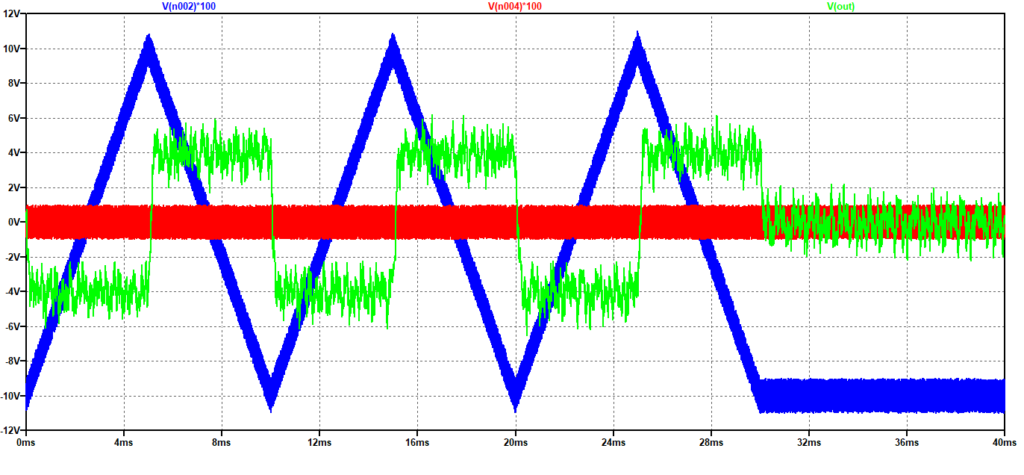 Figura 8: Risposta del derivatore passa-alto ad un’onda triangolare rumorosa
Figura 8: Risposta del derivatore passa-alto ad un’onda triangolare rumorosa
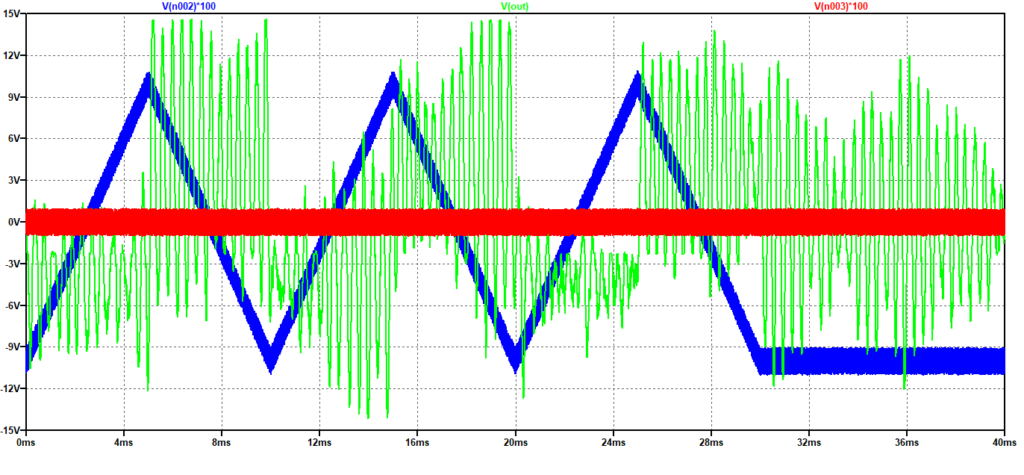 Figura 9: Risposta del derivatore ideale ad un’onda triangolare rumorosa
Figura 9: Risposta del derivatore ideale ad un’onda triangolare rumorosa
I miglioramenti ottenuti sono del tutto evidenti.
Il circuito sommatore
Dopo aver analizzato circuiti che agiscono su un solo segnale possiamo introdurre circuiti in grado di operare su più segnali in ingresso: una operazione “elementare” fra due segnali di cui si potrebbe aver bisogno in un dispositivo elettronico è la somma ed il circuito che vedremo è, quindi, un sommatore. Lo schema è mostrato in dove sono presenti due generatori in ingresso ma si può generalizzare anche a più sorgenti.
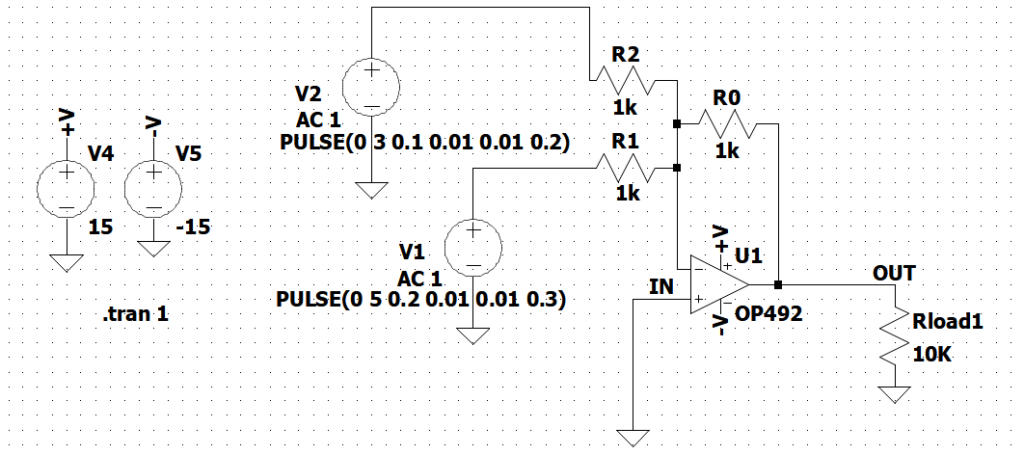 Figura 10: Circuito sommatore
Figura 10: Circuito sommatore
Grazie all’elevata impedenza di ingresso al morsetto invertente, applicando la legge di Kirchhoff ai nodi (la somma delle correnti entranti è nulla) possiamo dire che tutte le correnti fornite dai generatori confluiscono nel ramo di retroazione, ovvero nella resistenza R0. Per la presenza del corto circuito virtuale in ingresso all’OpAmp abbiamo anche che le correnti erogate dai generatori sono indipendenti fra loro e sono pari a in=Vn/Rn dove il pedice n è 1 o 2 a seconda del generatore considerato. Di conseguenza:
Vout = -R0 i0 = -R0 (V1/R1 + V2/R2)
Se le resistenze sono tutte uguali si ha:
Vout = – (V1 + V2)
cioè la tensione di uscita è la somma segnali in ingresso (cambiata di segno). Ovviamente si possono aggiungere più sorgenti, oppure usare resistenze di valore diverso per pesare in modo differente i segnali, a seconda del progetto che si vuole realizzare.
In si riporta il risultato della simulazione con con due ingressi sinusoidali sfasati di 90°.
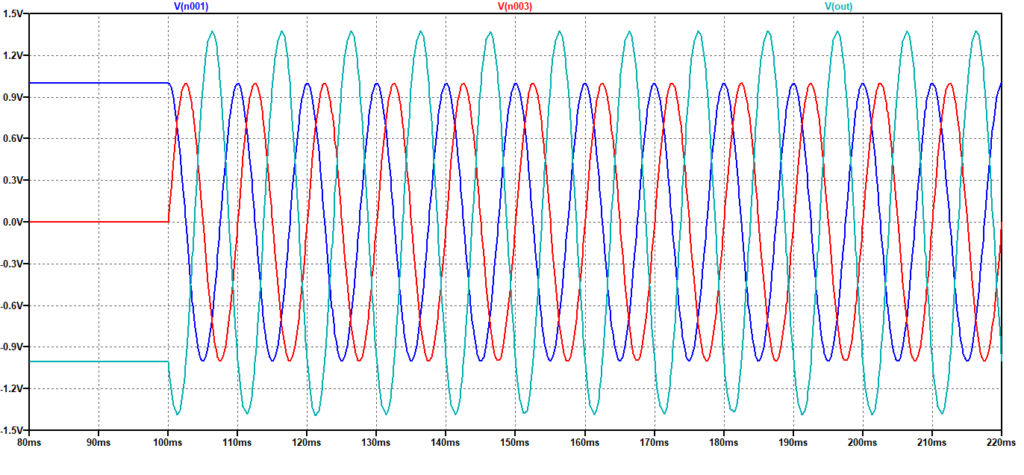 Figura 11: Somma di due sinusoidi sfasate
Figura 11: Somma di due sinusoidi sfasate
La somma di due segnali tipo impulsi rettangolari, di ampiezza e durate diverse è riportata nella successiva.
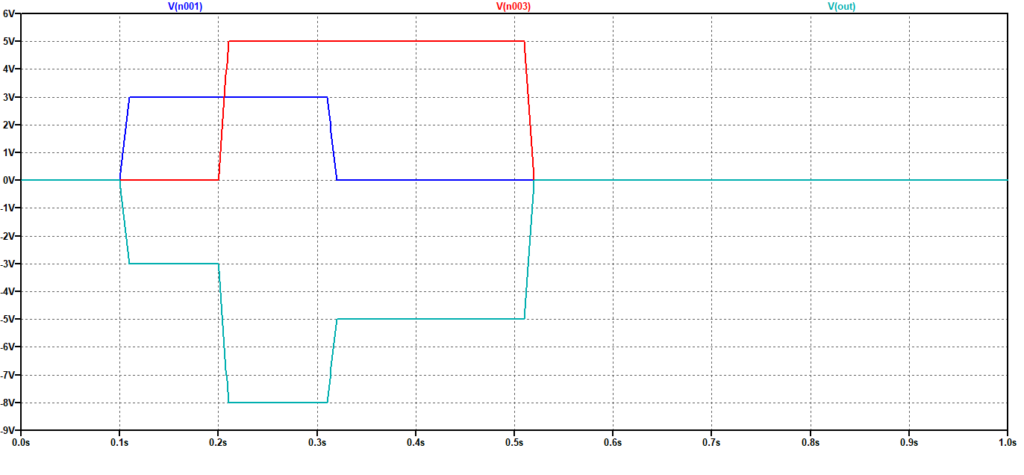 Figura 12: Somma di impulsi rettangolari
Figura 12: Somma di impulsi rettangolari
Conclusioni
In questo articolo abbiamo analizzato un circuito in grado di effettuare la derivata del segnale in ingresso evidenziandone i limiti e proponendo una possibile modifica in grado di rendere il circuito utilizzabile in pratica. In particolare abbiamo visto che il derivatore amplifica il rumore in alta frequenza e che, nella effettiva realizzazione con Amplificatori Operazionali reali ci possono addirittura essere oscillazioni indesiderate. La soluzione classica che si adotta consiste nell’inserire una resistenza in serie alla capacità in modo da realizzare un filtro passa-alto che approssima il derivatore per frequenze inferiori alla sua banda passante.
Un’altra utile applicazione dell’OpAmp in configurazione invertente è la somma di segnali in ingresso. Scegliendo le resistenze in serie agli ingressi di valore diverso si possono amplificare in modo diverso i segnali invece di effettuare una semplice somma.

















