I movimenti di una persona possono essere rappresentate mediante formule matematiche. Con l’aiuto di TuringBot è possibile tradurre in numeri tutti i movimenti che compie tale persona. Se i movimenti sono semplici, anche le formule saranno semplici. Al contrario, movimenti complessi possono essere descritte da formule ed equazioni più lunghe e complesse. Grazie alla possibilità di trovare le formule matematiche per qualsiasi tipo di azione, si possono implementare sistemi robotici, simulazioni, creazione di prototipi 3D, video giochi e molto altro.
Trasformare la vita reale in numeri e formule
Per descrivere il movimento di una persona (o di un animale, pianta oppure un oggetto) al computer occorre seguire diverse fasi e rappresentare matematicamente l’insieme delle azioni che egli compie. Alcuni passi sono abbastanza complicati. Questo articolo è dedicato alla rappresentazione numerica dei movimenti di un uomo che esegue l’esercizio fisico “Jumping Jack”. Le fasi da seguire sono le seguenti:
- acquisizione del video;
- taglio del video e mantenimento dei soli fotogrammi utili;
- identificazione delle parti del corpo in movimento;
- determinazione delle coordinate dei vari segmenti;
- regressione simbolica e curve fitting dei dati;
- applicazione delle formule e creazione di un modello 3D;
- creazione animazione finale e raffronto con il video originale.
Acquisizione del video e selezione dei fotogrammi
Per questa fase occorre creare un video della persona in movimento. Non è necessario che esso sia molto lungo. Sono sufficienti 3 o 4 secondi, anche a 15 FPS. L’importante è acquisire la sequenza dei fotogrammi utili, in cui l’atleta si muove per un periodo completo, ossia da quando il corpo umano assume una determinata posizione a quando esso ritorna alla stessa posizione.

figura 1 animazione
Occorre utilizzare probabilmente diversi software. Durante la creazione del video l’importante è che l’atleta sia ben illuminato e visibile e, soprattutto, l’angolo di ripresa non deve cambiare. Occorre tagliare il video in modo da prendere solo la sequenza utile. Per questo esempio, il video è composto da 29 fotogrammi. I vari elementi, quindi, sono rappresentati da altrettante posizioni nel dominio spaziale bidimensionale.

Figura 2: sequenza
Identificazione delle parti in movimento del corpo
Lo scopo del nostro lavoro è quello di simulare al computer il movimento di un oggetto grafico composto semplicemente da alcuni segmenti. A noi interessa, infatti, l’aspetto matematico della problematica e non quello grafico. L’atleta digitale deve essere realizzato mediante alcuni segmenti che rappresentano le braccia, le gambe, ecc. Di seguito possiamo osservare l’atleta assieme al suo virtuale “avatar”, composto da tanti segmenti che, successivamente, saranno processati matematicamente. Per comodità, l’avambraccio e la mano sono stati trattati come un unico segmento, dal momento che il video li rappresenta entrambi con un’unica linea.
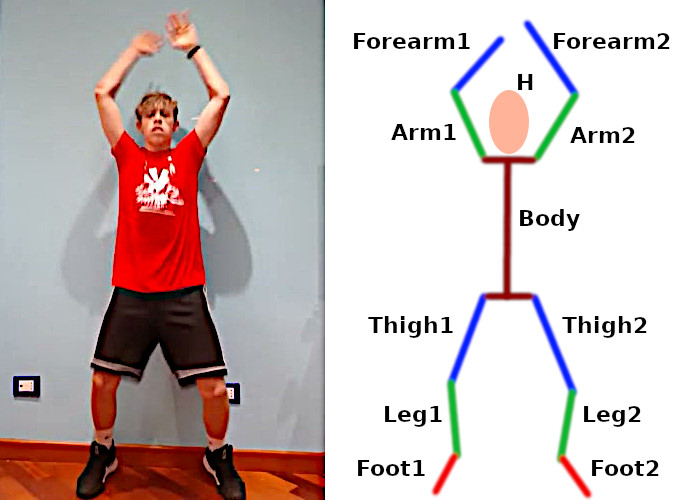
Figura 3: segmenti
L’atleta virtuale è composto dai seguenti elementi:
- un cerchio “H” per la testa, ossia un cerchio con posizione X, Y e raggio R;
- da due segmenti “Arm1” e “Arm2” per le braccia;
- da due segmenti “Forearm1” e “Forearm2” per gli avambracci;
- dal segmento “Body” per il corpo;
- da due segmenti “Thigh1” e “Thigh2” per le cosce;
- da due segmenti “Leg1” e “Leg2” per le gambe;
- da due segmenti “Foot1” e “Foot2” per i piedi.
Determinazione delle coordinate dei vari segmenti
La determinazione di tutte le coordinate dei punti del soggetto è la fase più importante e faticosa di tutta l’operazione. Un buon risultato dipende dalla precisione con cui sono stati presi i valori dei punti. Per ogni fotogramma occorre:
- determinare la coordinata X e Y di inizio di un segmento;
- determinare la coordinata X e Y di fine dello stesso segmento.
La testa è disegnata con un cerchio, per cui il suo centro (e la sua posizione) è rappresentato da un unico punto, con coordinate X e Y. Per valutare la posizione di ogni punto possiamo utilizzare qualsiasi programma di grafica, per esempio ImageJ che, in tempo reale, mostra la posizione del mouse (in pixel) sulla barra di stato e che ha tante ottime funzioni automatizzate di selezione che semplificano tanto lavoro. Noi utilizziamo tale informazione per ottenere le coordinate dei vari segmenti.
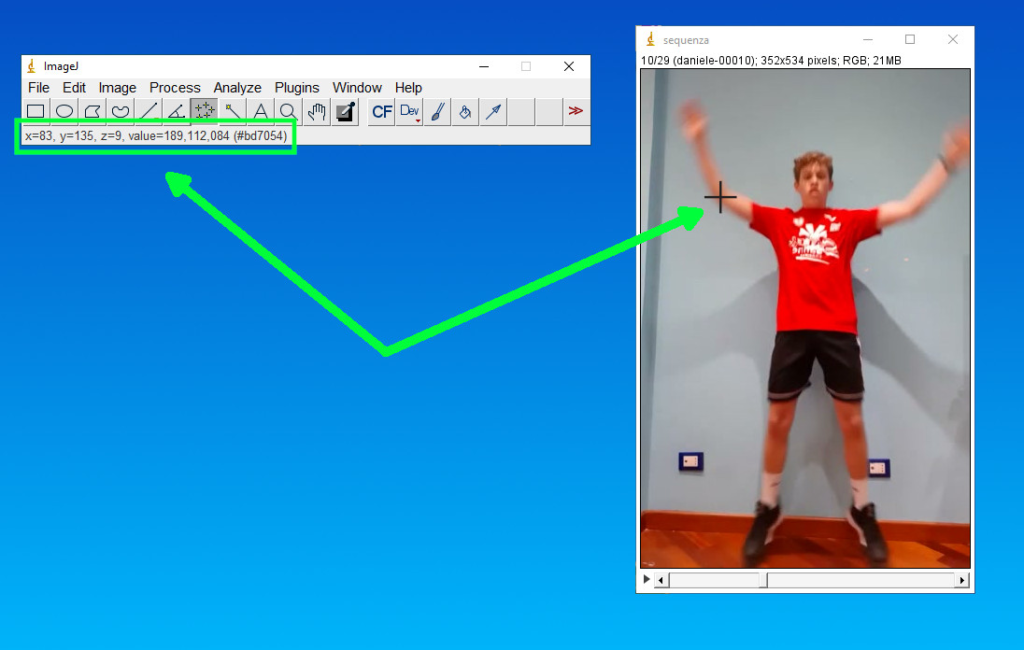
Figura 4: coordinate
Si tratta di un lavoro un po’ lungo, dove è richiesta la massima precisione e tanta pazienza. Alla fine dei calcoli è possibile inserire i risultati in un foglio elettronico. Si ricorda che queste coordinate sono relative. Per trasformarle in coordinate assolute è sufficiente sottrarre un valore fisso.
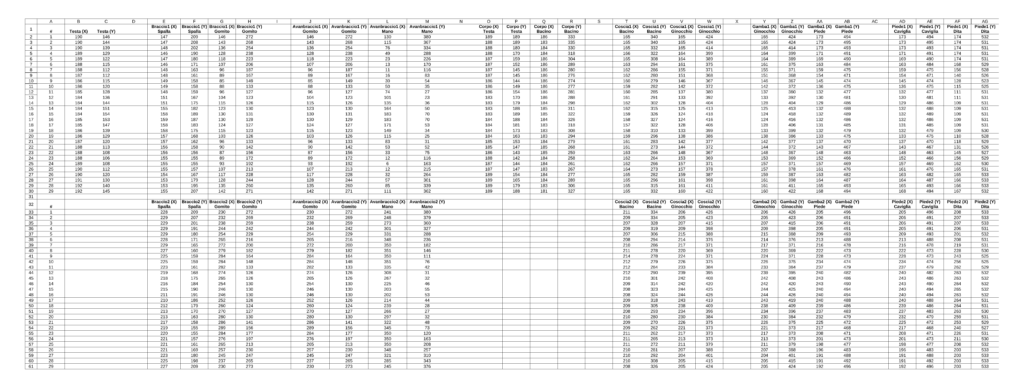
Figura 5: foglio elettronico
Con tutti questi dati a disposizione è possibile, ad esempio, tracciare i grafici di spostamento di alcuni elementi del corpo, per scoprire la presenza di eventuali anomalie. Per esempio, il grafico che segue mostra l’andamento della posizione nell’asse X e nell’asse Y, durante l’intero movimento di tutti i fotogrammi.
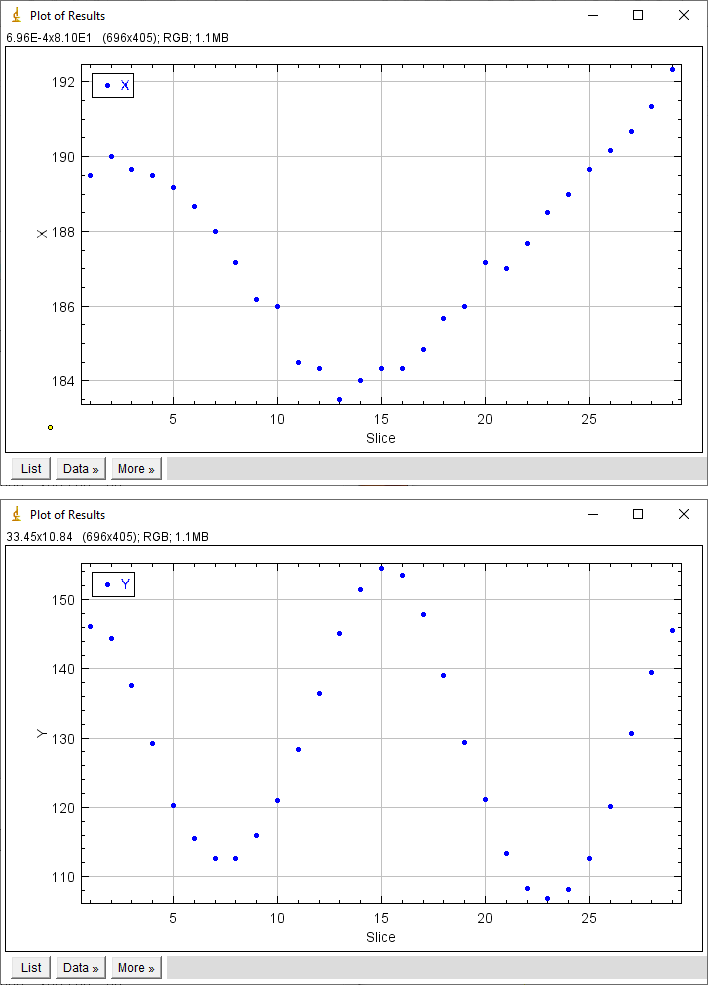
Figura 6: grafici dei movimenti
E adesso, TuringBot in azione
Tutte queste coordinate devono essere trasformate in formule matematica, anche se la via più semplice e sicura sarebbe quella di inserirle in un array e processare i movimenti all’interno di un loop. Ma l’adozione di equazioni e formule rende l’operazione molto più elegante e veloce, nonché permette la scrittura di un codice sorgente più corto e più compatto, con meno consumo di memoria. E’ sottinteso che se i movimenti dell’atleta cambiano, anche le formule dovranno seguire le stesse modifiche. E’ il momento giusto, dunque, di cercare di rappresentare gli andamenti dei movimenti dell’uomo con delle formule matematiche. I vari nodi del corpo umano sono rappresentati da tanti punti, dei quali occorre memorizzare le due coordinate X e Y. Occorre generare, dunque, una notevole quantità di formule matematiche che consentano di ottenere un piccolo miracolo aritmetico. Alcuni punti sono in comune, pertanto utilizzano le stesse formule.

Figura 7: punti
Per ogni coordinata di ogni punto occorre creare un file di testo per TuringBot, contenente due colonne. I dati sono presi, ovviamente, dal gigantesco foglio elettronico. Mostriamo qui sotto l’esempio per la coordinata X della testa, ma gli altri files seguono la stessa regola.
x y
1 190
2 190
3 190
4 189
5 189
6 188
7 188
8 187
9 186
10 186
11 185
12 184
13 184
14 184
15 184
16 185
17 185
18 186
19 186
20 187
21 188
22 188
23 188
24 189
25 190
26 190
27 191
28 192
29 192
Il setting di TuringBot è il seguente:
- Search metric: RMS error;
- Train/test split: No cross validation;
- Test sample: Chosen randomly;
- Integer constants only: Disabled;
- Bound search mode: Deactivated;
- Maximum formula complexity: 60;
- Allowed functions: + * / sin cos exp log sqrt abs floor ceil round
Per alcuni sistemi occorre fare attenzione con le funzioni trigonometriche. Esse lavorano in radianti in TuringBot, mentre per altri software grafici esse potrebbero lavorare in gradi, complicando il processo di conversione. Nel nostro caso specifico, sono state create le seguenti funzioni di conversione in OpenSCAD:
function cos_deg(x)=cos(x*180/3.1415);
function sin_deg(x)=sin(x*180/3.1415);
Per ogni formula è sufficiente un tempo di ricerca relativamente basso, diciamo 5-10 minuti o anche meno sono più che sufficienti. E’ molto interessante osservare TuringBot durante la ricerca. Le sue formule si avvicinano sempre più all’obiettivo finale, come è possibile vedere nella videata sotto.
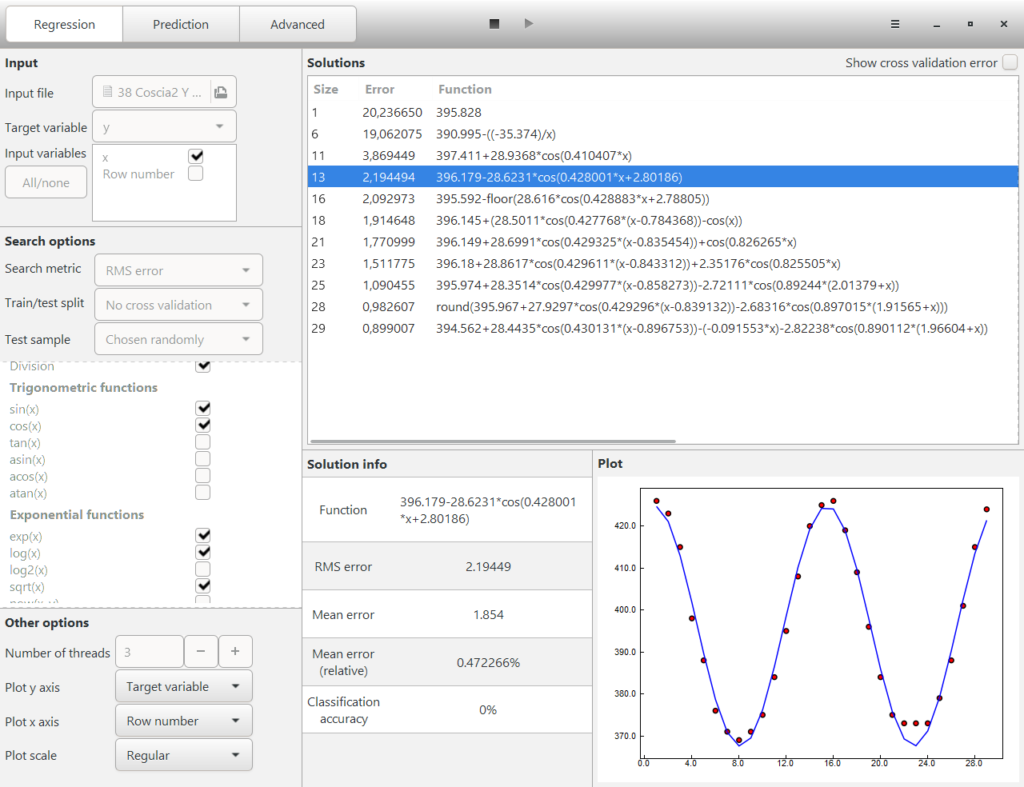
Figura 8: ricerca
Di seguito sono riportate tutte le formule che descrivono le posizioni di tutte le coordinate dei segmenti che costituiscono l’atleta virtuale.
| Head |
| y01=round((2.6318+(0.0554792*((0.624893-cos(5.98948*x))*x)))*cos(0.22113*x)+187.659); |
| y02=131.133+round((22.2134-cos(-0.236286+1.0202*x))*cos((-0.0920179)*(((-6.27235+cos(1.1767+x))/x)+200.387*x))-cos(0.665542+0.98184*x)+(-0.312138*x)+4.11456); |
| Arm 1 |
| y03=145.872-((-0.162146)*3.12725*round(cos(0.869371-round(5.96336*x))*(0.362323*x+1.77951)-(cos(-2.63665+round(-0.806851*x))/0.61255)+x)); |
| y04=191.306+((round(cos(0.100135*(-8.17967-1.70143*round(cos(x))+x))*(1.27238*x-cos(-1.86063+x))-(cos(389.994*(x+1.88321)+0.0989649)/0.0417673))+x)/(-1.2269)); |
| y05=round((-22.0364+ceil(-0.00500284*ceil(x)*x))*(-1.65113-cos(19.3301*(x-0.0605927))))+((30.7797/(0.161422+x))+(68.1958-cos(51.0009*x))-cos(x)); |
| y06=exp(3.04946+cos(2.45808*(-0.0870771*x)+0.138404)+1.14937)+(98.0591+round(sin(round(0.980629*x)))+((6.65119-cos(exp(0.0876617*x)))*cos(0.695886*(2.86001+x)))); |
| Forearm 1 |
| y07=y05; |
| y08=y06; |
| y09=(82.9424-5.26613*cos(0.586505*x))*(cos((-0.373595)*(x+exp(round(0.702127*x)-(0.498511+round(0.81141*x)))+1.08672))+1.09296)-cos(x+1.33121); |
| y10=24.2181-floor((6.34302+(-0.112064*x))*round(cos(0.553976+x)))+abs(12.7211+x-((0.650495*x-11.0444)*round(3.27817*((cos((-0.730758)*(0.273942+x))/0.755489)+(x-12.8353))))); |
| Body 1 |
| y11=2.89195*cos(1.94668*0.118136*floor(0.631336-(0.929462*x+cos(exp(0.91244*x))))+(0.00305925/cos(x)))+186.109; |
| y12=round(168.264-(ceil(23.9806*cos((-2.32409+(-0.00596887+x))/0.00939977))+1.57128*cos(-1.18468*x))-(cos(x)+(1.91115*(cos(7.08496*(-0.288919+x))+0.109288*x)))); |
| y13=round(185.474-0.0754086*x)+round(cos((-0.991109+0.0450943*x)*(0.928695*x+log(x)))); |
| y14=302.57-round(0.656922*x)-(3.72319*cos(0.92024*(0.811155+x))+round((0.357329-x*cos(0.448989*(5.09698+x)))*(-0.0148642*x+((-0.214389*cos(61*x)*(4.88954-x)-25.1065)/x)))); |
| Thigh 1 |
| y15=(3.73138+((-2.81755)/x)-1.5051*sin(round(0.797607*x+0.247816)+3.30139))*(-0.514093+cos(0.205523*(cos(round((-4.32537)*(x+((-1.0676)/x))))+x)))+164.175; |
| y16=round(291.396-((0.865647*x+13.9971)*cos(x+568-0.562408*x)))-3.78295*cos(0.889973*(1.67606+x))-((-68.1261)/(1.44242*cos(x-0.362494*x)+x)); |
| y17=18.9883*cos(-12.8305*floor(-2.33066+x))+(0.0747105*(7.00189-(0.0741629/cos(x))+x)*cos(509.575*x))+(148.027+round(cos(x+0.658366))+(-0.209201*round(x))); |
| y18=390.962+(round((-0.602733)*(cos(0.747127*x-0.621592)+0.177481)*(-13.466-cos(round((-0.957067)/cos(x)))+cos(x*x)+x))+27.0249*cos(0.457091*(-0.671057+(2.28055-x)))); |
| Leg 1 |
| y19=y17; |
| y20=y18; |
| y21=((4.54964+(-0.104918*x)+0.86746)*cos(0.908546*x+2.08515)+22.7637)*cos(-0.111712*cos(0.935385*x)+6.70845*0.0314056*1*x)+(155.963-(x/3.08672)); |
| y22=(13.6737-round((x-1.93818)*(0.289077+cos(-0.619872+x))))*(-0.0369057+round(3.95993/(x+1.89954)))+478.649+round(cos(0.116577*(-3.69209*x))*round(0.549631*(2.80209+x))); |
| Foot 1 |
| y23=y21; |
| y24=y22; |
| y25=139.272+round(41.4532+(5.65241*cos(1.93845+0.927451*x)+(-0.313033*x)))*cos(0.233247*(cos(0.93121*(0.497331+x))+(1.53881-x))); |
| y26=round(0.608219/x)+(round(531.435-exp(sin((-0.579902)*(-1.04537+x))-round(cos((-0.437731)*(-1.0422+x)))))-1.74977*round(-0.0192443*x)); |
| Arm 2 |
| y27=215.61+(round(-6.43715+((0.0859084*x-cos(0.942479-x))*cos(x-1.00562)))*cos((0.294155+(-0.00453909*cos(x)))*(4.12657+x))+round(16.3707/(1.00701+0.237835*x))); |
| y28=11.6855*cos(0.807271*x-x)+round((cos((-0.423063)*(x-0.93908))/(0.0525671+(-0.000435858*x)))-log(x)*cos(0.888721*(2.08408+x)))+178.346; |
| y29=268.152-cos(x)-round(cos(13.3713*x))-round((2.85905+(cos(x/0.00529412)+(30.6583/x)))*(cos((-0.503562)*(3.04348+x))/(-0.441047+0.0116418*x))); |
| y30=round(190.29-((0.274471*(x-1.03236)-cos(x)+4.1627)*cos(0.498517*(x+3.46653))))+((77.1759+8.48446*cos(-0.610676*x))*cos(-0.201617*x)); |
| Forearm 2 |
| y31=y29; |
| y32=y30; |
| y33=round(-0.249366*x)+291.228+(-12.6244*cos((-0.820511)*(-0.186609+x)))-(round(78.0757*cos((-0.404411)*((2.17112/(x+0.071869))+x-0.610615)))-ceil(4.08193*cos((-1.17325)*(x-0.515673)))); |
| y34=abs(164.762+(224*cos(0.198515*x)-15.9158*cos((-0.738632)*(1.55249+x)))-8.63263*cos(-1.01382*x*cos(0.211738*x)+0.224974))-3.18017+6.85659*cos(x); |
| Thigh 2 |
| y35=0.172415+round(210.278+1.65102*round(cos(5.80056*(0.885518+x)))+(-0.0412545*x+cos(6.98431*x)))+floor(((-0.0356155)/sin(x-18.9299))+0.158463); |
| y36=round(round(3.61529*cos(round(0.194003*x))+(307.838-3.51777*cos((-0.897347)*(1.61609+x)))-0.729957*x)-cos(0.471091*(5.10132+0.942463*x))*round(21.5251+0.421583*round(x))); |
| y37=221.338-19.8608*cos(0.208955*x)+3.4534*cos(0.449626*(cos(2.00243*x*cos(x))+(-1.68947+x))); |
| y38=(0.247935/(-0.632871+x-3.60529))+(395.163+((28.4837+cos(exp(x+0.642375)))*cos(0.430087*(x-0.908733)))-ceil(-0.0921263*x))-round(2.63053*cos(0.886319*(2.07703+x))); |
| Leg 2 |
| y39=y37; |
| y40=y38; |
| y41=221.068-round(cos((-0.229646)*(1.00585-x))*(0.512421*x+(17.4901+((3.61754-3.39247*cos(round(0.966905*x)))*cos(-0.599782*x-(-970.82-x)))))); |
| y42=round(((7.16092*cos(x)+2.62982)/x)+ceil(11.2742*cos(0.46229*round(2.61198-1.01162*x))))+round(1.6828*cos(23.8215*(0.0290402+x)))+481.601; |
| Foot 2 |
| y43=y41; |
| y44=y42; |
| y45=233.767+((-30.4935+cos(1.96625*x))*cos((-0.253376)*(2.19983-(0.927354*x-2.38703*cos(0.421426*x-1.58061))))); |
| y46=530.782+((cos(0.663909*x)+cos(2.00314*x)+2.30646)*cos(0.509108*(3-x))+round(cos(0.471645-x))); |
Implementazione del modello
Dopo la creazione delle formule da parte di TuringBot, è possibile finalmente implementare il modello matematico dell’atleta. La figura sotto mostra l’utilizzo di OpenSCAD con le equazioni create.
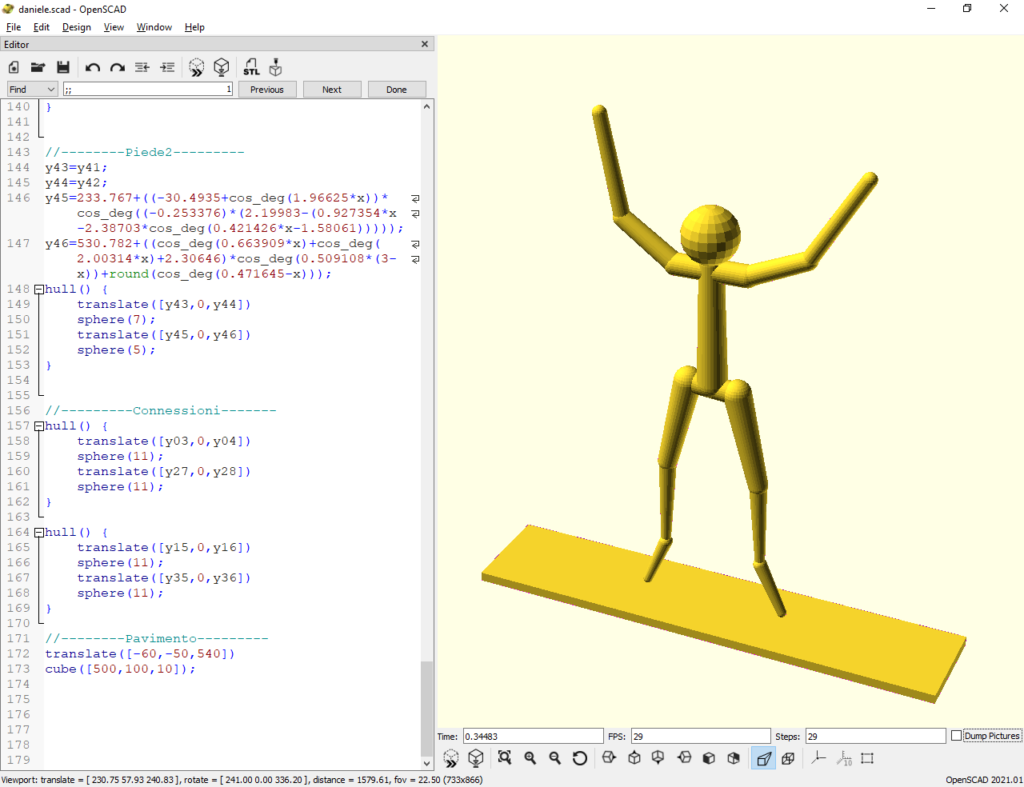
Figura 9: implementazione
Il seguente breve elenco mostra tutti software utilizzati nel progetto. Ovviamente l’utente può usare altri software, secondo le proprie necessità.
- registratore video di uno smartphone o telecamera;
- Avidemux;
- ImageMagick (convert.exe);
- ImageJ;
- Calc (LibreOffice);
- e naturalmente… TuringBot.
E’ molto interessante osservare l’animazione del soggetto reale e di quello virtuale, nello stesso momento.

Figura 10: modello reale e virtuale
Conclusioni
Con la regressione simbolica è possibile convertire qualsiasi fatto e azione in formula matematica. Queste tecniche sono utilizzate nei film, nei videogiochi e nelle simulazioni 2D e 3D. Dietro un brevissimo filmato, anche della durata di un solo secondo, c’è tanta fatica e decine di ore di lavoro. L’adozione di formule matematiche per la descrizione dei punti, nello spazio 2D e 3D, conferisce un grande tocco di eleganza al progetto. A seconda dei software utilizzati potrebbe essere necessario “ribaltare” le coordinate del soggetto. Tutta la procedura descritta è stata molto appassionante e divertente, anche se molto faticosa. E la soddisfazione è stata immensa quando, dopo tutti i calcoli effettuati e l’implementazione del codice, il personaggio digitale ha acquisito una vita propria e ha iniziato a saltare. Ricordiamolo ancora una volta, il movimento dell’atleta non è prodotto da coordinate memorizzate in un array, ma è creato tramite formule matematiche. Tutta questa enorme elaborazione non sarebbe stata possibile senza l’utilizzo di TuringBot. Questa è matematica!

Figura 11: animazione finale















